Дифференциальное уравнение стержня потерявшего устойчивость

Рассмотрим стержень, защемленный одним концом и шарнирно опертый на другом. Приложим продольную силу 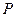. Отклоним его от положения равновесия и рассмотрим равновесие отсеченной части.

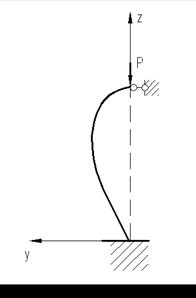
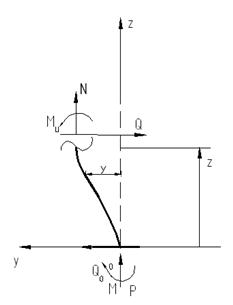
Рис. 8.3

Выпишем дифференциальное уравнение, изогнутой оси стержня.

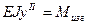
Изгибающий момент в произвольном сечении 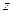, равен

,

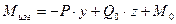где .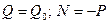

.

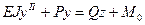Получим линейное неоднородное уравнение второго порядка. Продифференцировав его два раза по 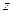придем к однородному.

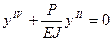
или

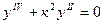, (8.1)

где 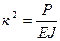(8.2)

Общий интеграл уравнения (8.1) имеет вид

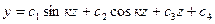(8.3)