Задача Эйлера об устойчивости шарнирно опертого стержня сжатого силой Р
Дифференциальное уравнение (8.1) имеет решения (8.3). Найдем постоянные интегрирования 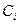 из граничных условий для шарнирно опертого стержня (рис. 8.4).
из граничных условий для шарнирно опертого стержня (рис. 8.4).
При 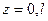
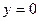 или
или 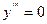
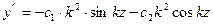
1). 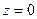 2).
2). 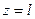
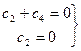
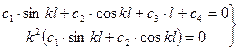
Откуда: 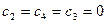
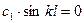
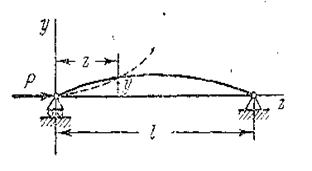
Рис. 8.4
Если 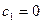 , то получим тривиальное решение, т.е. устойчива только прямолинейная форма равновесия.
, то получим тривиальное решение, т.е. устойчива только прямолинейная форма равновесия.
При 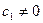 , имеем
, имеем
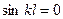 откуда
откуда  , где
, где 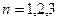
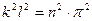 , но
, но 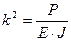
Тогда получим
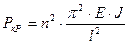 , (8.4)
, (8.4)
где 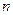 — число полуволн (рис. 8.5)
— число полуволн (рис. 8.5)
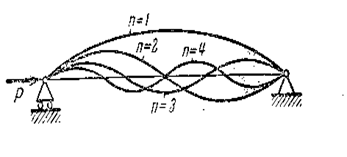
Рис. 8.5
Минимальное значение критической силы будет при 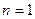 . В итоге получим формулу критической силы для шарнирно опертого стержня.
. В итоге получим формулу критической силы для шарнирно опертого стержня.
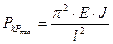 (8.5)
(8.5)
На рис. 8.6 показаны различные случаи закрепления сжатого стержня. Для каждого случая необходимо проводить решение, как это сделано в предыдущем параграфе. Решение этих задач показало, что всех случаев, изображенных на рисунке, критическую силу можно определять по обобщенной формуле.
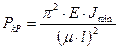 , (8.6)
, (8.6)
Где 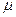 — коэффициент приведенной длины, а величина
— коэффициент приведенной длины, а величина 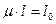 — приведенная длина. Приведенная длина
— приведенная длина. Приведенная длина 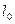 — условная длина шарнира опертого стержня, имеющего такую же критическую нагрузку, как заданный стержень. В отдельных случаях это видно из геометрии.
— условная длина шарнира опертого стержня, имеющего такую же критическую нагрузку, как заданный стержень. В отдельных случаях это видно из геометрии.
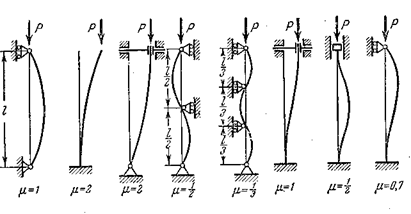
Рис. 8.6
 2014-02-02
2014-02-02 769
769








