Пусть некоторая точка движется по окружности радиуса r. Изменение положения точки в пространстве за промежуток времени D t определяется углом поворота 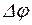 (рис. 3). Элементарный поворот на угол
(рис. 3). Элементарный поворот на угол 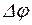 можно рассматривать как вектор
можно рассматривать как вектор 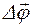 . Модуль вектора
. Модуль вектора 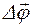 равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружн
равен углу поворота, а его направление совпадает с направлением поступательного движения острия правого винта, головка которого вращается в направлении движения точки по окружн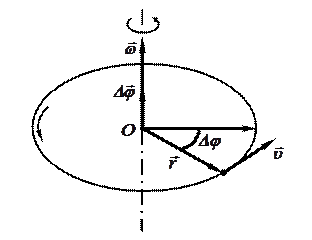 ости, т.е. подчиняется правилу правого винта.
ости, т.е. подчиняется правилу правого винта.
Рис. 3
Угловой скоростью 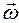 называется векторная величина, равная пределу отношения угла поворота
называется векторная величина, равная пределу отношения угла поворота 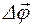 к промежутку времени D t, за который этот поворот произошел, при стремлении D t к нулю:
к промежутку времени D t, за который этот поворот произошел, при стремлении D t к нулю:
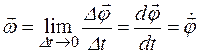 ,
,
где 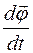 – первая производная от функции угла поворота
– первая производная от функции угла поворота 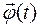 радиус-вектора
радиус-вектора 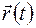 по времени t. Эту производную принято обозначать, как
по времени t. Эту производную принято обозначать, как 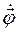 .
.
Вектор 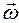 направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
направлен вдоль оси вращения в соответствии с правилом правого винта (рис. 3).
Угловым ускорением 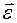 называется векторная величина, равная пределу отношения изменения угловой скорости
называется векторная величина, равная пределу отношения изменения угловой скорости 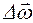 к промежутку времени D t, за который это изменение произошло, при стремлении D t к нулю:
к промежутку времени D t, за который это изменение произошло, при стремлении D t к нулю:
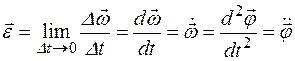 ,
,
где 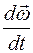 – первая производная от функции
– первая производная от функции 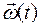 по времени t,
по времени t,
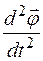 – вторая производная от функции
– вторая производная от функции 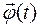 по времени t.
по времени t.
Эти производные принято обозначать соответственно в виде: 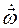 и
и 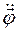 .
.
Вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном вращении направление вектора 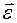 совпадает с направлением вектора угловой скорости
совпадает с направлением вектора угловой скорости 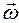 , а при замедленном – противоположно ему.
, а при замедленном – противоположно ему.
Кинематические параметры поступательного и вращательного движения связаны между собой. Связь скорости 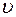 и угловой скорости
и угловой скорости 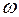 (см. рис. 3) определяется следующим образом:
(см. рис. 3) определяется следующим образом: 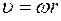 .
.
В векторном виде эту связь для векторов 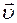 и
и 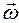 можно записать с помощью векторного произведения:
можно записать с помощью векторного произведения: 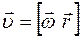 .
.
Ускорение а также можно выразить через угловые параметры, разложив ускорение а на две составляющие 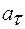 и
и 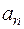 , то есть:
, то есть: 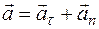 .
.
Тангенциальная составляющая 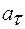 выражается через угловое ускорение
выражается через угловое ускорение 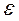 :
:
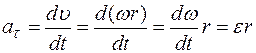 ,
,
а нормальная составляющая 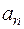 – через угловую скорость
– через угловую скорость 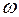 :
:
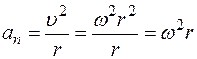 .
.
Тогда ускорение: 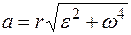 .
.
 2014-02-02
2014-02-02 2091
2091








