Внутренняя энергия реального газа

Внутренняя энергия идеального газа целиком определяется кинетической энергией теплового движения молекул и зависит только от его температуры:

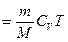, (2.5.6)

где – молярная теплоемкость газа при постоянном объеме, 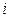– число степеней свободы молекул газа.

При вычислении внутренней энергии реальных газов необходимо также учитывать потенциальную энергию 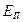, обусловленную силами межмолекулярного взаимодействия

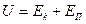. (2.5.7)

Силы молекулярного сцепления вызывают появление дополнительного внутреннего давления (2.5.2) , а их работа приводит к изменению потенциальной энергии

Проинтегрируем полученное выражение

.

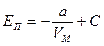При безграничном увеличении объема расстояния между молекулами возрастают и потенциальную энергию следует принять равной нулю, поэтому и постоянная интегрирования 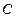принимает нулевое значение ().

Складывая кинетическую и потенциальную энергии, получим, что, внутренняя энергия реального газа зависит от его температуры 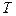и объема :

. (2.5.8)

Из первого закона термодинамики (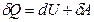) следует, что при адиабатном расширении газа (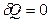) без совершения работы (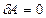) (расширение газа в вакуум)

и .

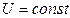внутренняя энергия газа не изменяется.

Это равенство формально справедливо, как для идеального, так и для реального газов, но его физический смысл для обоих случаев различен.

Для идеального газа равенство 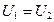означает равенство температур (), т. е. при адиабатном расширении идеального газа в вакуум его температура не изменяется.

Из уравнения (2.5.8) следует, что внутренняя энергия реального газа не изменится, если адиабатное изменение его объема будет сопровождаться изменением температуры газа, причем 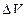и 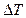будут иметь разные знаки.Следовательно, при адиабатном расширенииреального газа в вакуум он охлаждается, а при адиабатном сжатии в вакуум – нагревается.

Контрольные вопросы:

1. Какие величины, которыми пренебрегают, рассматривая идеальные газы, учитывает уравнение Ван-дер-Ваальса?

2. От каких параметров состояния зависит внутренняя энергия ван-дер-ваальсовского газа?

3. Могут ли существовать в равновесии жидкая вода, ее пар и две кристаллические модификации льда?

Лекция № 5.