2014-02-02
822
V. Рееальные газы и пары
Понятие об идеальном газе, являясь удобной абстракцией дало возможность построить молекулярно-кинетическую теорию, рассмотреть явления переноса, вопросы вычисления теплоемкостей и др. В определенных рамках выводы этой теории хорошо подтверждаются экспериментально.
Приневысоких давлениях и температурах разреженные газы по своим свойствам хорошо приближаются к идеальному. При больших давленияхвозникает значительное сжатие газа, и суммарный объем молекул становится сравнимым с объемом, занимаемым газом. Кроме того, сближение молекул при сжатии газа приводит к заметному проявлению сил межмолекулярного взаимодействия.
В уравнении, описывающем состояние реального газа, должны быть учтены объем молекул и силы межмолекулярного взаимодействия. Поэтому голландским физиком Ван-дер-Ваальсом были внесены две поправки в уравнение состояния идеального газа. Рассмотрим их.
1. Учет собственного объема молекул
При сближении частиц возрастают силы отталкивания. Они противодействуют взаимному проникновению молекул в занятые ими пространства. Поэтому свободный объем, в котором могут двигаться молекулы реального газа, должен быть уменьшен на величину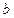 
, пропорциональную их собственному объему. Следовательно, вместо величины 
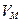в уравнении состояния следует поставить величину (
). (2.5.1)
|
|
|
Постоянная 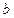должна быть больше суммарного объема всех молекул газа, т. к. даже при плотной «укладке» молекул-шариков между ними остаются незаполненные промежутки.
2. Учет притяжения молекул
Силы взаимного притяжения молекул приводят к появлению дополнительного давления на газ, называемого внутренним давлением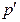 
. Поэтому в уравнении состояния давление 
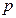следует заменить величиной (
).
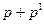По вычислениям Ван-дер-Ваальса внутреннее давление пропорционально квадрату концентрации молекул или обратно пропорционально квадрату молярного объема газа ()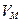
, (2.5.2)
где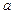 
– постоянная величина, зависящая от природы газа.
Введя обе поправки в уравнение Клапейрона, получим уравнение состояния 1 моля реального газа (уравнение Ван-дер-Ваальса):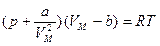 
. (2.5.3)
Для произвольного количества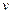 
газа (
) можно записать
, (2.5.4)
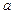где и 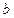– постоянные величины, определяемые экспериментально; 
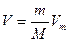– объем, занимаемый газом. Уравнение Ван-дер-Ваальса также является приближенным, т. к. при его выводе был сделан целый ряд упрощений. Это не единственное уравнение, описывающее реальные газы. Существуют и другие, но они не рассматриваются из-за их сложности.
