
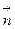 Пусть мы имеем элементарную площадку dS,
Пусть мы имеем элементарную площадку dS,


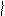 a нормаль
a нормаль 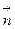 к которой в месте расположения
к которой в месте расположения
dS 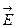 площадки, составляет с вектором
площадки, составляет с вектором 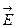 угол a.
угол a.
(рис. 14.5). Элементарным потоком dФ сквозь
Рис.14.5 площадку dS называют величину
dФ = E · dS · cosa = En dS = 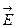 ·
·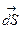 ,
,
где En - проекция вектора 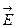 на направление нормали
на направление нормали 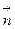 к площадке,
к площадке, 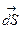 - вектор, модуль которого равен dS, а направление совпадает с нормалью
- вектор, модуль которого равен dS, а направление совпадает с нормалью 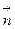 .
.
Для произвольной поверхности S поток вектора 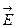 сквозь нее можно записать:
сквозь нее можно записать:
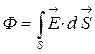 . (3.3.1)
. (3.3.1)
Следует отметить, что в случае замкнутых поверхностей за положительное направление нормали 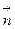 берется внешняя нормаль, т.е. направленная наружу поверхности.
берется внешняя нормаль, т.е. направленная наружу поверхности.
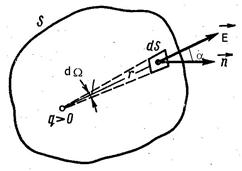 |

 Рис.14.6
Рис.14.6
Рассмотрим поле одного точечного заряда q (рис.14.6). Проведем вокруг этого заряда произвольную замкнутую поверхность и найдем поток вектора 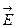 сквозь площадку
сквозь площадку 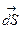
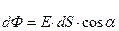 .
.
Подставив значение Е для точечного заряда, тогда последнюю формулу можно записать:
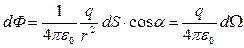 , (3.3.2)
, (3.3.2)
где 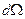 - телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения заряда q. Интегрируя выражение (3.3.2) по всему телесному углу мы получим
- телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения заряда q. Интегрируя выражение (3.3.2) по всему телесному углу мы получим 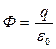 и заменив левую часть этого уравнения по (3.3.1) имеем:
и заменив левую часть этого уравнения по (3.3.1) имеем:
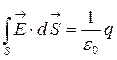 .
.
Если заряд охватывает поверхность любой формы, то угол a может принимать значения больше p / 2, а значит, cosa и 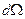 могут принимать значения, как больше нуля, так и меньше нуля. Отсюда следует, что если заряд расположен вне замкнутой поверхности, то поток вектора
могут принимать значения, как больше нуля, так и меньше нуля. Отсюда следует, что если заряд расположен вне замкнутой поверхности, то поток вектора 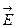 через нее равен нулю. В случае, когда поле создается системой точечных зарядов q1, q2¼ qn то в соответствии с принципом суперпозиции (3.2.4)
через нее равен нулю. В случае, когда поле создается системой точечных зарядов q1, q2¼ qn то в соответствии с принципом суперпозиции (3.2.4) 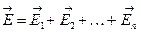 поэтому:
поэтому:
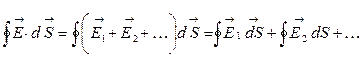 .
.
Каждый интеграл в правой части равен qi /eо, если заряд qi находится внутри замкнутой поверхности. Поэтому в правой части предыдущего уравнения мы должны записать алгебраическую сумму зарядов qi, находящихся внутри поверхности S. Таким образом окончательно можно записать:
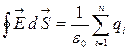 . (3.3.3)
. (3.3.3)
Данное уравнение математически выражает теорему Гаусса. Ее можно сформулировать так: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри данной поверхности, деленной на e0. Если заряды распределены непрерывно с объемной плотностью  , то суммарный заряд, находящийся внутри замкнутой поверхности, охватывающий объем V
, то суммарный заряд, находящийся внутри замкнутой поверхности, охватывающий объем V :
:
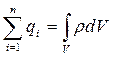 . (3.3.4)
. (3.3.4)
Используя формулу (3.3.4) теорему Гаусса можно записать:
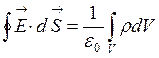 . (3.3.5)
. (3.3.5)
 2014-02-02
2014-02-02 538
538







