2014-02-02
904
Пример лингвистической переменной:
Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий:
«Малая толщина», «Средняя толщина», «Большая толщина»
При этом минимальная толщина = 10 мм, а максимальная = 80 мм.
Формализация такого описания может быть определена с помощью следующей лингвистической переменной:
(x,T,U,G,M)
x – толщина изделия;
T – термо множество {«Малая толщина», «Средняя толщина», «Большая толщина»};
U – отрезок от 10 до 80;
G – процедура образования новых термов с помощью связок «И», «ИЛИ». и модификаторов типа «очень», «не», «слегка», и т.д. Например: «Малая или средняя толщина», «очень малая толщина»;
М – процедура задания на U = [10,80] нечётких подмножеств
А1 = «Малая толщина», А2 = «Средняя толщина», А3 = «Большая толщина»
а также нечётких множеств для термов G(T) в соответствии с правилами трансляции нечётких связок и модификаторов «И», «ИЛИ», «НЕ», «ОЧЕНЬ», «СЛЕГКА» и других операций над нечёткими множествами вида:
;
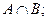
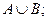
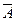CON A =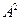 
– растяжение;
DIL A = 
– сжатие.
Терма множество и расширенное терма множество в условиях примера можно характеризовать следующими функциями принадлежности:
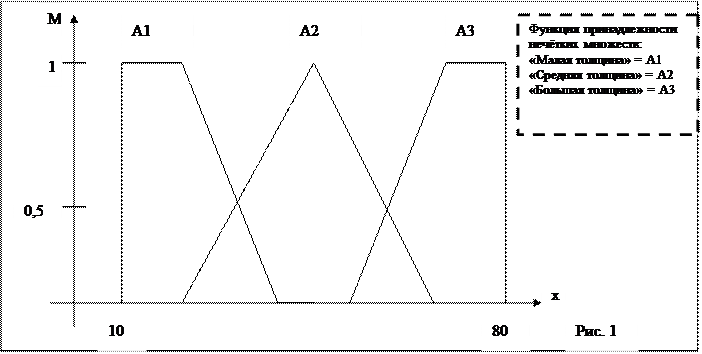
На рисунке 2 приведена функция принадлежности нечёткого множества «Малая или средняя толщина»:
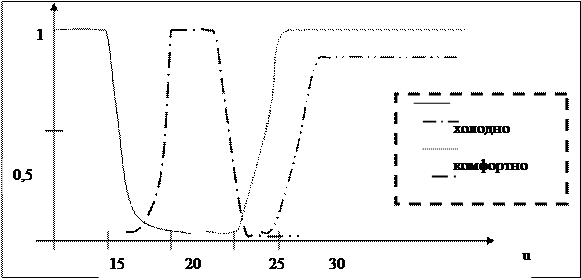
Рассмотрим лингвистическую переменную с именем x = «температура в комнате»,
тогда оставшуюся четвёрку чисел в определении лингвистической переменной можно определить так:
U = [12, 35]
T = {«Холодно», «Комфортно», «Жарко»} со следующими функциями принадлежности:
;
;
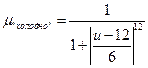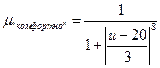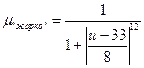
G – синтаксические правила G порождающие новые термы с использованием квантификаторов «не», «очень», «более-менее».
М – семантические правила М заданные в таблице 1:
| Правило модификации функции принадлежности | |
| Кванитификатор | Функция принадлежности |
Не  |  |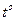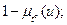
| Очень |  |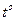
| Более-менее |  |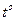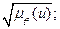
Нечёткая истинность
Особое место в нечёткой логике занимает лингвистическая переменная истинность.
В классической логике истинность может принимать только 2 значения:
«Истинно»;
«Ложно».
В нечёткой логике истинность «размытая». Нечёткая истинность определяется аксиоматически, причём разные авторы делают это по-разному.
[0,1]- этот интервал используется как универсальное множество лингвистической переменной истинность.
Обычная чёткая истинность может быть представленная нечёткими множествами – синглтонами. В этом случае, чётким понятиям «Истинно» и «Ложно» будут соответствовать функции принадлежности
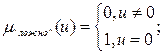
Для нечёткой истинности Лотфи Заде предложил следующую функцию принадлежности термов «Истинно» и «Ложно»:
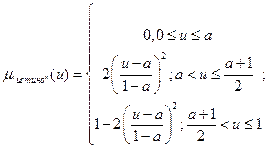
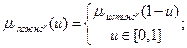
Параметр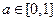 
– он задаёт носителей нечёткого множества «истинно» и «ложно»
Для нечёткого множества истинно носителем будет интервал (a,1].
Для нечёткого множества ложно носителем будет интервал [0,a).
графики функции принадлежности нечётких термов «Истинно» и «Ложно», при а = 0,4
имеют вид:
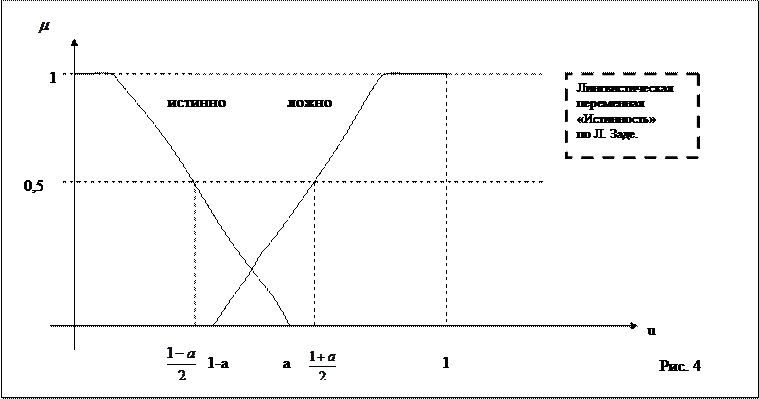
Балдин предложил другие функции принадлежности для нечётких значений «Истинно» и «Ложно».
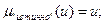
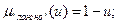
функция принадлежности новых термов рассчитываются с использованием операций концентрации, что соответствует возведению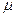 
в квадрат и операция DIL, что соответствует возведение в степень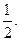 
; 
; 
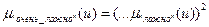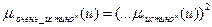
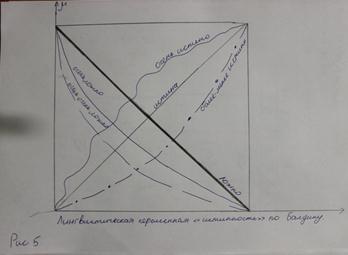
Нечёткие логические операции
Нечёткие логические операции:
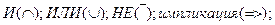
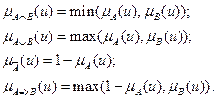
в нечёткой логике количество возможных значений истинности может быть бесконечно,
поэтому в общем виде табличное представление логических операций невозможно. Однако таблицей можно задать нечёткую логическую операцию, при ограниченном числе истинностных значений.
Для логики с 3 нечёткими значениями истинности
{T – «истинно», F – «Ложно», T+F – «Неизвестно»} Заде предложил следующую лингвистическую таблицу истинности:
| A | B | |  |  |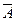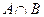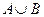
| T | T | F | T | T |
| T | F | F | F | T |
| T | T+F | F | T+F | T |
| F | T | T | F | T |
| F | F | T | F | F |
| F | T+F | T | F | T+F |
| T+F | T | T+F | T+F | T |
| T+F | F | T+F | F | T+F |
| T+F | T+F | T+F | T+F | T+F |
