Структура сети Петри. Сети Петри специально разрабатывались для моделирования систем, которые содержат взаимодействующие параллельные компоненты большой сложности

Сети Петри

Сети Петри специально разрабатывались для моделирования систем, которые содержат взаимодействующие параллельные компоненты большой сложности.

Впервые сеть Петри предложил Карл Адам Петри (ФРГ) 1962г.

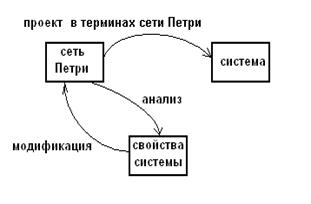
Применение при проектировании и анализе систем (2 подхода).

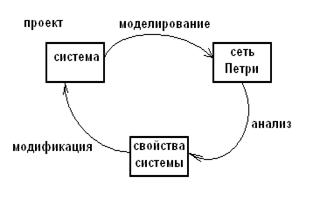
Сеть Петри состоит из четырех компонентов С = (P, T, I, O).

P – множество позиций,

T – множество переходов,

I – входная функция,

O – выходная функция.

Пример сети.

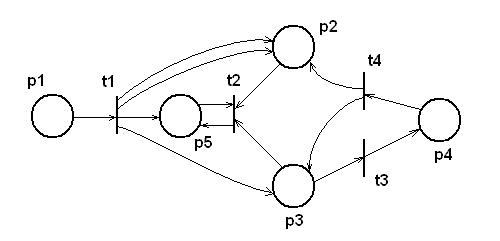
C = (P, T, I, O).

P = {p1, p2, p3, p4, p5} - позиции,

T = {t1, t2, t3, t4} - переходы.

Входная функция показывает, из каких позиций и сколько дуг входит в данный переход.

I(t1) = {p1},

I(t2) = {p2, p3, p5}, p1 … p5 – входные позиции перехода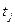

I(t3) = {p3},

I(t4) = {p4}.

Выходная функция показывает в какие позиции и сколько дуг выходит из данного перехода.

O(t1) = {p2, p2, p3, p5},

O(t2) = {p5}, p1 … p5 – выходные позиции перехода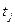

O(t3) = {p4},

O(t4) = {p2, p3}.

Расширенные входные и выходные функции (вх/вых функции относительно позиций).

#(tj, I(pi)) = #(pi, O(tj)),

#(tj, O(pi)) = #(pi, I(tj)).

Для рассмотренной сети Петри расширенными входными и выходными функциями являются

I(p1) = {}, I(p2) = {t1, t1, t4}, I(p3) = {t1, t4}, входные функции I(p4) = {t3}, позиций I(p5) = {t1, t2}

O(p1) = {t1}, O(p2) = {t2}, O(p3) = {t2, t3}, выходные функции O(p4) = {t4}, позиций O(p5) = {t2}.