Элементы теории комплектов

Описание систем сетями Петри

Для того, чтобы представить ИС и моделировать перемещение потоков данных в ней с помощью сетей Петри, необходимо ознакомиться с понятиями теории комплектов.

Теория комплектов (ТК) это расширение теории множеств. В комплекте допускается несколько экземпляров одного и того же элемента.

Пример: Задана область объектов { a, b, c, d }

B1 = {a, b, c}. B2 = {a}. B3 = {a, b, c, c}. B4 = {a, a, a}. B5 = {b, c, b, c}.

B6 = {c, c, b, b}. B7 = {a, a, a, a, a, b, b, c, d, d, d, d, d, d}.

Здесь,

B1, B2 – множества.

B5, B6 – один и тот же комплект.

Основное понятие ТК – число экземпляров #(x, B), читается «число x в B»

Например: 0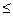#(x, B) 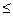1, получим множество B, т.к. ограничили число экземпляров одним элементом.

Мощность |B| = 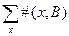 общее число экземпляров в комплекте.

Пусть A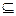B. A подкомплект B.

Тогда #(x,A) 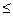#(x,B) для всех x.

Над комплектами справедливы следующие операции.

Объединение комплектов

A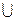B: #(x, A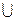B) = max(#(x,A), #(x,B)).

Пересечение комплектов

A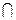B: #(x, A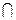B) = min(#(x,A), #(x,B)).

Сумма комплектов

A+B: #(x, A+B) = #(x,A) + #(x,B).

Разность комплектов

A-B: #(x, A-B) = #(x,A) - #(x, A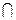B).