2014-02-02
307
Самым распространенным методом оценки параметров уравнения регрессии является МНК. Для использования МНК необходимо, чтобы были выполнены все предпосылки МНК. МНК заключается в минимизации суммы квадратов отклонений между эксперементальными и расчетными значениями, то есть SSост.
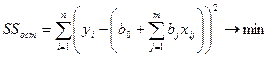
Необходимым условием минимума является равенство 0 всех частных производных.
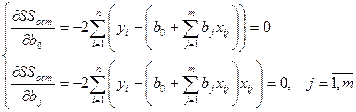
Решение такой системы можно представить в векторной форме.
Y = XB + E,
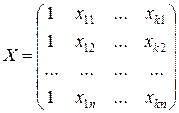
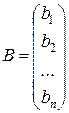
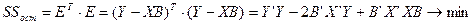
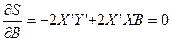
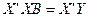
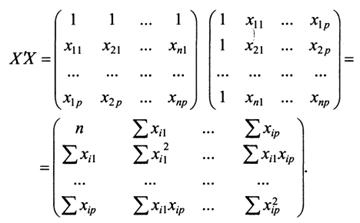
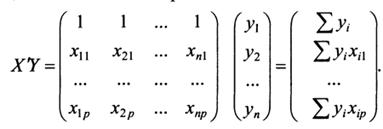
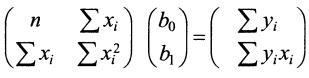
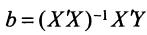(1)
Так, для уравнения y = a + b 1 × x 1 + b 2 × x 2 + … + bp × xp + e система нормальных уравнений составит:
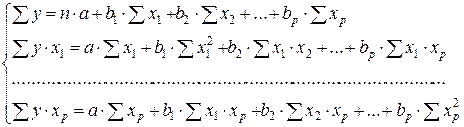(1)
Её решение может быть осуществлено методом определителей:
a = Da / D, b 1 = Db 1 / D,…, bp = Dbp / D,
где D – определитель системы; Da, Db 1, …, Dbp – частные определители.
При этом
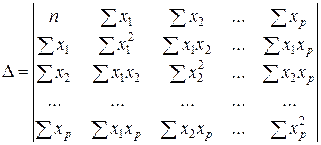
а Da, Db 1, …, Dbp получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Например, для двух факторов
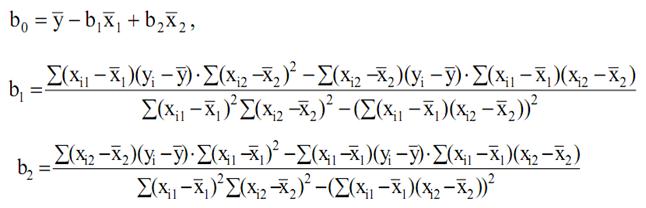
Пример 3.4. Имеются следующие данные по 10 предприятиям концерна о прибыли (y – млн. руб.), выработке продукции на одного работника (x 1 – единиц) и доле продукции, производимой на экспорт (x 2 – %), приведенные в табл. 3.1.
Таблица 3.1. Исходные и расчетные данные для примера построения множественной регрессии
| № п/п | y | x 1 | x 2 | y 2 | x 12 | x 22 | yx 1 | yx 2 | x 1 x 2 | yr |
| 2,284553 | ||||||||||
| 1,45935 | ||||||||||
| 3,109756 | ||||||||||
| 8,060976 | ||||||||||
| 6,544715 | ||||||||||
| 4,174797 | ||||||||||
| 3,934959 | ||||||||||
| 5,585366 | ||||||||||
| 6,890244 | ||||||||||
| 7,955285 | ||||||||||
| Итого |
Система нормальных уравнений составит:
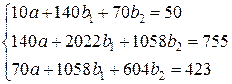
Решая ее методом определителей, получим:
D = 9840, Da = –47960, Db 1 = 5760, Db 2 = 2360,
откуда:
a = –4,874; b 1 = 0,585; b 2 = 0,240.
Уравнение регрессии выглядит следующим образом:
y = –4,874 + 0,585 × x 1 + 0,240 × x 2 + e.
Расчетные значения прибыли приведены в последнем столбце таблицы.
Также найти решение уравнения (1) можно искать непосредственно по формуле
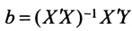, где ‘ – транспонированная матрица.
