Критерий устойчивости Найквиста для импульсных систем

Критерий устойчивости Найквиста так же как и для непрерывных систем позволяет судить об устойчивости замкнутой импульсной системы по амплитудно-частотной характеристике (АЧХ), или годографу Найквиста, разомкнутой импульсной системы. При этом АЧХ может быть построена экспериментально.

По аналогии с критерием для непрерывных систем сформируем функцию.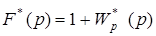

С учетом равенства ,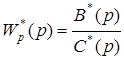

где 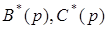- полиномы от 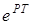степени m и n соответственно (m_n),

можно записать

.

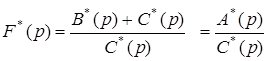Таким образом, функция 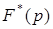связывает характеристический полином замкнутой импульсной системы 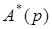с характеристическим полиномом разомкнутой системы .

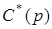Так же как и для случая непрерывных систем, найдем приращение аргумента вектора 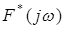при изменении частоты в диапазоне : .

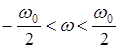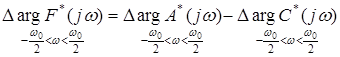или в диапазоне : .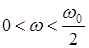

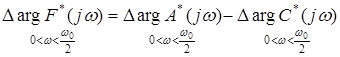Поскольку мы интересуемся условиями устойчивости замкнутой системы, при выполнении которых все n корней характеристического полинома 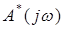лежат внутри окружности единичного радиуса, то в соответствии с принципом аргумента для импульсных систем

.

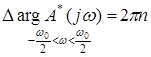
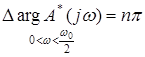Для определения приращения аргумента вектора 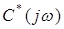рассмотрим три случая:

a) a) Разомкнутая импульсная система устойчива, т.е. все n корней ее характеристического полинома лежат внутри окружности единичного радиуса. Тогда в соответствии с принципом аргумента

и

а приращение аргумента функции 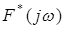будет равно нулю в соответствии с выражениями

и

.

Рассмотрим геометрическую интерпретацию этой ситуации.

На рис.1.11 а представлен график функции 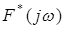, для которой изменение аргумента при изменении частоты в диапазоне 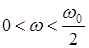равно нулю, а на рис. 1.11 б - график соответствующей ей .

а б