Интегральное исчисление функции одной переменной.
Психофизиология восприятия и порождения речи.
Психофизиология эволюционных посылок речи.
Это про первую, вторую и промежутчную сигнальные системы. Павлов, Орбелли, эксперименты с обезьянами, проект «Уошо» и т.п. Самое главное – смысл экспериментов. Про дискуссию Хомского и Пиаже толком не рассказывали. Но в общих чертах: Хомский за врожденную грамматику, Пиаже многое выводил из внешней среды и опыта. Язык как инстинкт – это название книжки Пинкера. Он доказывает, что язык – наше видовое качество.
Про межполушарную асимметрию у животных – это разговор о «предспециализации» полушарий.
Еще надо не забыть про подкорковые механизмы речи. В частности, связанные с лимбической системой. Отсюда мост к эмоциональным вокализациям у животных.
По анатомии можно грубо выделить два уровня: связок и всей остальной артикуляции. Формация – это образование голоса. Артикуляция – изменение конфигурации рта, которое изменяет итоговый спектр.
Всё, я устала писать.
Рассмотрим операцию обратную к дифференцированию, которая называется интегрированием и состоит в отыскании функции по ее производной. К ней приводят многие задачи из физики.
Определение 1. Функция 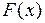 называется первообразной функции
называется первообразной функции 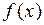 на промежутке
на промежутке 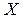 , если
, если 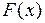 дифференцируема на этом промежутке и
дифференцируема на этом промежутке и
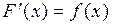
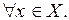
Определение 2. Множество всех первообразных функции 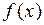 на про- межутке
на про- межутке 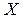 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 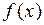 на множестве
на множестве 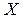 и обозначается
и обозначается 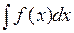 .
.
Теорема. Если 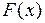 есть первообразная функции
есть первообразная функции 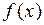 на промежутке
на промежутке 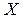 , то
, то
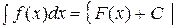
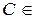 R
R 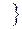 . (1)
. (1)
Обычно формулу (1) записывают в следующем виде:
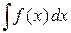 =
=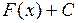 .
.
Из таблицы производных получается таблица неопределенных интегралов:
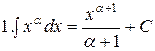
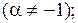


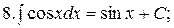
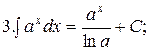
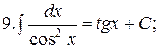
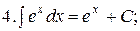

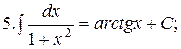
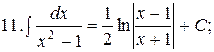
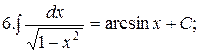
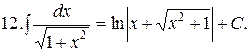
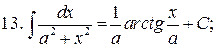
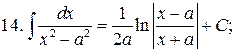
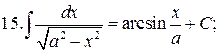
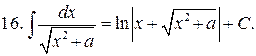
Эти формулы легко доказать непосредственным дифференцированием.
Замечание 1. Все неопределенные интегралы в таблице рассматриваются на промежутках, на которых определены все функции, входящие в соответствующую формулу.
Теорема 1. Постоянный множитель можно вынести за знак интеграла:
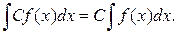
Теорема 2. Интеграл от суммы или разности равен сумме или разности интегралов:
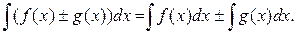
Доказательства теорем 1 и 2 получаются непосредственно из определения 2 и соответствующих свойств производной.
Пример 1. 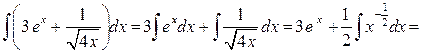


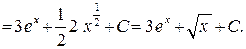

Теорема 3. Пусть функции 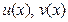 и их производные
и их производные 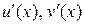 непрерывны на промежутке X. Тогда на этом промежутке
непрерывны на промежутке X. Тогда на этом промежутке
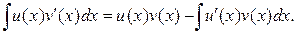
Замечание 1. Формула (2) называется формулой интегрирования по частям. Из определения дифференциала функций следуют равенства:
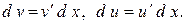
Отсюда и из (2) получим формулу интегрирования по частям в дифференциальной форме:
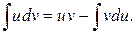 (3)
(3)
Замечание 2. При использовании формулы (3) полезна таблица дифференциалов, которая в ходе решения задач читателями может быть расширена:
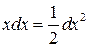 ,
, 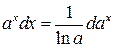 ,
, 
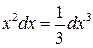 ,
,

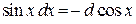 ,
,  ,
, 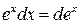 ,
,
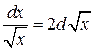 ,
, 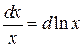 (на промежутке (0, +
(на промежутке (0, + )).
)).
Замечание 3. При выборе функций u и v в формуле интегрирования по частям рекомендуется использовать следующие соображения. Пусть подынтегральная функция представлена в виде произведения двух функций. Тогда в качестве функции u нужно взять ту из них, которая упростится после взятия производной. Оставшийся множитель следует внести под знак дифференциала (при этом можно использовать таблицу дифференциалов). Функция, оказавшаяся после этого под знаком дифференциала, будет являться функцией v.
Пример. 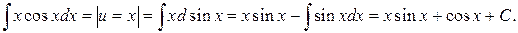
Теорема 4. Пусть функция f (u) непрерывна на промежутке U, а функция u=φ (x) отображает промежуток X в промежуток U и 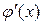 существует и сохраняет постоянный знак на промежутке X. Тогда на X
существует и сохраняет постоянный знак на промежутке X. Тогда на X
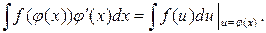 (4).
(4).
Замечание 1. Формула (4) называется формулой замены переменной. Для того, чтобы пользоваться таблицей дифференциалов, эту формулу удобно применять в следующей форме:
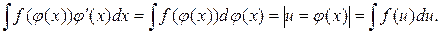 (7).
(7).
Замечание 2. При использовании формулы (7) можно применять следующие свойства дифференциала:
I. Постоянный множитель можно вынести из под знака дифференциала;
II. Под знаком дифференциала можно прибавить и отнять константу.
Замечание 3. Внесение функции под знак дифференциала можно выполнять с помощью неопределенного интеграла.
 2014-02-02
2014-02-02 636
636







