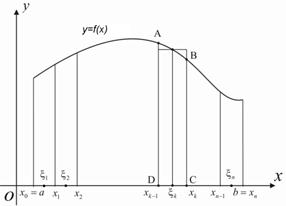
Пусть функция 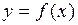 непрерывна на отрезке
непрерывна на отрезке 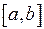 . Разобьем отрезок
. Разобьем отрезок 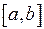 на
на 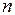 отрезков точками
отрезков точками 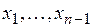 таких, что
таких, что 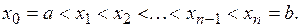 Множество точек
Множество точек 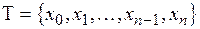 называют разбиением отрезка
называют разбиением отрезка 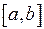 ; Обозначим
; Обозначим 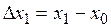 ,
, ,
,  ,
, 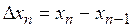 ,
, 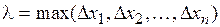 - диаметр разбиения
- диаметр разбиения 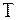 . Очевидно, что
. Очевидно, что 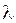 зависит от
зависит от 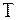 . Это записывают так:
. Это записывают так: 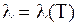 . Выберем на
. Выберем на
каждом отрезке  по одной точке
по одной точке 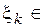
 , где
, где  . Точки
. Точки  называют промежуточными точками. Обозначим множество промежуточных точек буквой
называют промежуточными точками. Обозначим множество промежуточных точек буквой 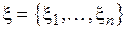 .
.
Обозначим 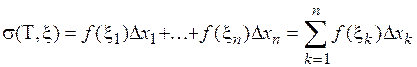 .
.
Величина 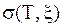 называется интегральной суммой функции
называется интегральной суммой функции 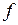 , соответствующей данному разбиению
, соответствующей данному разбиению 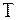 и промежуточным точкам
и промежуточным точкам 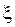 . Каждое слагаемое интегральной суммы
. Каждое слагаемое интегральной суммы 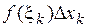 представляет собой площадь прямоугольника, которая приблизительно равна площади криволинейной трапеции ABCD. Поэтому вся сумма
представляет собой площадь прямоугольника, которая приблизительно равна площади криволинейной трапеции ABCD. Поэтому вся сумма 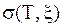 дает приближенное выражение для площади криволинейной трапеции, ограниченной графиком функции
дает приближенное выражение для площади криволинейной трапеции, ограниченной графиком функции 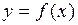 и прямыми
и прямыми 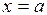 ,
, 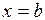 ,
, 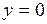 (в случае, когда
(в случае, когда 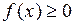
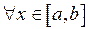 ). Очевидно, что это приближение тем точнее, чем мельче разбиение
). Очевидно, что это приближение тем точнее, чем мельче разбиение 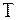 , то есть чем меньше диаметр разбиения
, то есть чем меньше диаметр разбиения 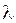 .
.
Определение 1.Число I называют пределом интегральных сумм 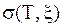 при
при 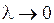 и при этом пишут
и при этом пишут
I 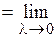
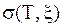 или
или 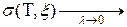 I, (10)
I, (10)
если 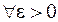
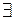 разбиение
разбиение 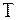 такое, что для любого выбора промежуточных точек
такое, что для любого выбора промежуточных точек 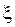 имеет место неравенство
имеет место неравенство 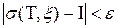 .
.
Замечание 1. В курсе математического анализа доказывается существование предела (10), если функция 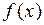 непрерывна на отрезке
непрерывна на отрезке 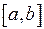 .
.
Определение 2. Предел при 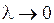 интегральных сумм I называется определенным интегралом Римана от функции
интегральных сумм I называется определенным интегралом Римана от функции 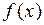 на отрезке
на отрезке 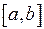 и обозначается
и обозначается 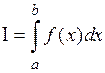 . Числа a и b называют нижним и верхним пределом интегрирования соответственно.
. Числа a и b называют нижним и верхним пределом интегрирования соответственно.
Непосредственно из определения выводятся следующие свойства определенного интеграла:
1. 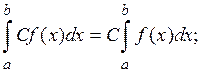
2. 
3. 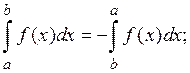
4. 
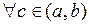 .
.
(Во всех формулах 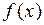 и
и  непрерывны на
непрерывны на 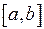 .)
.)
Связь определенного и неопределенного интегралов задается формулой Ньютона-Лейбница:
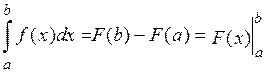 ,
,
где 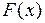 есть первообразная функции
есть первообразная функции 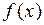 , непрерывной на отрезке
, непрерывной на отрезке 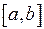 .
.
Отметим, что первообразная 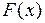 может быть найдена с помощью вычисления неопределенного интеграла. В курсе математического анализа доказано, что непрерывная на отрезке [ a,b ] функция имеет на нем первообразную. Одна из первообразных задается формулой
может быть найдена с помощью вычисления неопределенного интеграла. В курсе математического анализа доказано, что непрерывная на отрезке [ a,b ] функция имеет на нем первообразную. Одна из первообразных задается формулой 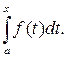
С помощью определенного интеграла можно решить такие задачи, как вычисление площади плоской фигуры, длины плоской кривой, объема тела вращения, площади поверхности тела вращения и другие. Приведем только три из перечисленных формул, которые будут нам необходимы при решении задач.
1. Площадь плоской фигуры, расположенной между прямыми 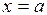 ,
,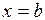 ,
, 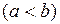 и графиками функций
и графиками функций 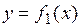 ,
, 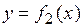 (где
(где 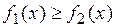
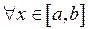 , см. рис.) задается формулой:
, см. рис.) задается формулой:
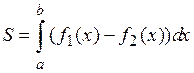 .
.
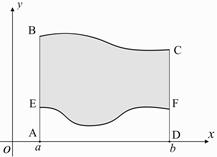 Эта формула легко вытекает из определения определенного интеграла и свойства 2.
Эта формула легко вытекает из определения определенного интеграла и свойства 2.
Действительно, площадь криволинейной трапеции ABCD равна: 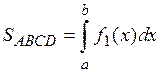 . Площадь криволинейной трапеции AEFD равна:
. Площадь криволинейной трапеции AEFD равна:
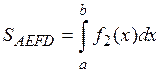 . Поэтому
. Поэтому 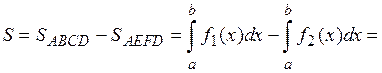
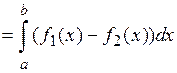 .
.
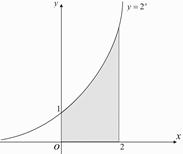 Пример. Найти площадь фигуры, ограниченной линиями
Пример. Найти площадь фигуры, ограниченной линиями 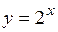 ,
, 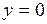 ,
,
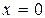 ,
, 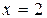 . (см. рис.)
. (см. рис.)
Решение.
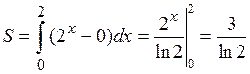
 2014-02-02
2014-02-02 2949
2949