Механизм течения полимеров

Согласно теории Я.И. Френкеля и Г. Эйринга течение жидкостей осуществляется перескоком отдельных молекул в соседнее положение, если оно свободно.

Перескоки эти происходят в жидкости всегда и в отсутствие течения просто под действием флуктуации тепловой энергии. Течение же возникает тогда, когда на жидкость действует некоторое напряжение τ, как это показано на рис. 38. Наличие напряжения делает более вероятными перескоки молекул в направлении действующего напряжения. Под действием флуктуаций тепловой энергии молекула 1 колеблется возле положения равновесия, причем число колебаний до перескока может быть велико и даже для низкомолекулярных маловязких жидкостей может составлять несколько тысяч. В некоторый момент времени происходит перескок молекулы 1 из положения 1 в положение 2 и перескок этот соответствует моменту, когда молекула накопила запас энергии, достаточный для преодоления взаимодействия с соседями.

Совершенно очевидно, что любой запас энергии недостаточен для перескока, если соседние с молекулой места заняты другими молекулами. Иными словами, для перескока необходимо наличие «дырки» по соседству с «горячей» молекулой. После перескока место 1 оказывается вакантным. Молекулы перемещаются в направлении напряжения τ, «дырки»- в обратном.

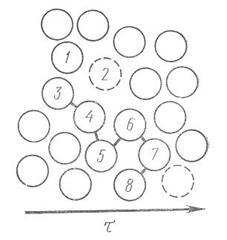Рис.38 Схема, поясняющая механизм течения низкомолекулярной жидкости под действием напряжения сдвига τ.

Особенность течения в полимерах состоит в том, что в них длинные гибкие цепные молекулы не могут перемещаться, как единое целое. Как упругая высокоэластическая деформация, так и деформация вязкого течения осуществляется путем последовательного перемещения сегментов макромолекул. Напомним, что сегмент- это часть молекулы, которая перемещается, как единое целое в элементарном акте теплового движения. Это значит, что макромолекула, являющаяся совокупностью сегментов 345678 (рис. 38) при наличии «дырки» в положении 2 может деформироваться так, что сегмент 3 перейдет в положение 2. Далее при наличии дырок по соседству с сегментами 7 или 8 произойдет их перемещение; на освободившееся место перейдут сегменты 5 или 6 и т. д., что приведет к смещению (вязкому течению) всей макромолекулы.

Сегмент макромолекулы тем легче перейдет в соседнее положение, чем больше запас тепловой энергии в системе, т.е. чем выше температура и чем слабее он связан с соседями как в своей макромолекуле, так и с сегментами соседних макромолекул. Это приводит к выражению для вероятности перескока сегмента:

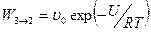(45)

Здесь ν₀– собственная частота колебаний сегмента возле положения равновесия, T- температура, R- газовая постоянная, а U- энергия связи одного моля сегментов с соседями. В полярном полимере U велико и вероятность перескока мала. Если число сегментов в макромолекулах двух сравниваемых полимеров одинаково, то вязкость больше у того из них, в котором меньше вероятность перехода сегмента в соседнее положение (W_3→2).

Многочисленные опыты показали, что сегменты перестают совершать тепловое перемещение в соседнее положение тогда, когда общий объем всех «дырок» (свободный объем) в полимере равен или меньше 2,5% от общего объема полимера. Когда свободный объем достигает этой величины, полимер переходит в стеклообразное состояние – всякое течение прекращается.

Таким образом течение полимера возможно в том случае, когда имеется достаточное количество дырок, т.е. достаточный свободный объем. Под действием напряжения сдвига в условиях, когда течение полимера возможно, сегменты макромолекулы перемещаются, некоторые узлы переплетений макромолекул распутываются и возникают в другом месте, т.е. флуктуационная сетка последовательно разрушается и создается вновь, разрушаются одни микрообласти ближнего порядка и создаются другие, в результате надмолекулярная структура в целом не меняется, но происходит течение, т.е. перемещение макромолекул, как результат последовательного перемещения сегментов.

Перемещение сегментов приводит не только к перемещению макромолекул, но и к их деформации. Молекулярные клубки постепенно вытягиваются и достигают определенной анизометричности или степени вытянутости, которая постоянна для данной скорости деформации и температуры и определяет величину эластической деформации текущего полимера. Снимем напряжение, деформация клубков исчезнет, что внешне выразится в упругом сокращении расплава. При этом вязкая деформация, конечно, сохранится.

Деформация клубков макромолекул обеспечивает эластическую деформацию расплава, достигающую нескольких сотен процентов. Это, однако, не приводит к столь существенному изменению надмолекулярной структуры расплава, чтобы вызвать зависимость вязкости от скорости или напряжения сдвига. Если полимер составлен из макромолекул одинаковой длинны (равной молекулярной массы), то скорость деформации оказывается строго пропорциональной напряжению сдвига, т.е. вязкость не зависит от напряжения сдвига (кривые 1 на рис.34 и 35).

Рис.39 Зависимость скорости сдвига и вязкости от напряжения сдвига τ. полные реологические кривые. Области напряжений сдвига I и III соответствуют течению с постоянной вязкостью; II – область структурной вязкости, где эффективная вязкость η зависит от напряжения сдвига.

В случае растворов полимеров общая деформация и ориентация клубков может и не приводить к потери раствором способности к течению. В этом случае при некотором напряжении сдвига достигается ситуация, когда надмолекулярные структуры (ассоциаты макромолекул) предельно разрушены, макромолекулы предельно ориентированы, структура раствора больше не меняется и вязкость снова перестает зависеть от напряжения сдвига. При этом можно получить так называемую полную кривую течения, показанную схематически на рис.39. На участке I и III раствор течет, как ньютоновская жидкость, однако надмолекулярная структура системы столь различна в этих двух состояниях, что по вязкости они могут различать в тысячи раз.