Реология полимеров
Совершено, очевидно, что большие обратимые деформации полимеров (т.е. способность проявлять высокоэластичность) не всегда являются достоинством для конструкционных материалов, а в тех случаях, когда полимерному материалу необходимо придать определенную форму. Заданная форма изделия наилучшим образом сохранится тогда, когда деформация расплава (или раствора) полимера истинно необратима, т.е. является деформацией вязкого течения. Поэтому практически все методы переработки полимеров в изделия (начиная от автопокрышек и кончая волокнами и пленками) основаны на переводе полимера в вязкотекучее состояние и придании ему формы именно в том состоянии, когда вся деформация полимера или ее большая часть является необратимой.
Отрасль науки, изучающая течение жидкостей, в которых наряду с вязкостью существует и обратимая деформация, носит название реологии от греческого слова «рео», что значит «течение», «течь».
Если при деформировании полимера преобладает необратимая деформация, то значит, полимер находится в вязкотекучем состоянии. Если полимер без разложения (термодеструкции) нельзя перевести в вязкотекучее состояние, то для переработки его предварительно растворяют, а затем, после придания формы, удаляют растворитель. Так перерабатывают полимеры, служащие как лаковые и защитные покрытия; очень часто к этому методу прибегают при получении волокон и пленок.
Реологическое поведение полимеров и их растворов определяется не только температурой, но и природой полимера, его молекулярной массой и молекулярно-массовым распределением (ММР), а также напряжением и скоростью сдвига, при которых осуществляется течение раствора или расплава. Поэтому нельзя характеризовать реологические свойства полимера по одной величине, скажем по величине вязкости. Охарактеризовать реологическое поведение полимера можно лишь установив зависимость вязкости от напряжения или от скорости сдвига и получив при этом кривые течения.
С этой точки зрения наиболее простым является случай, когда напряжение сдвига в полимере пропорционально скорости сдвига (кривая 1, рис. 34). С ростом напряжения сдвига пропорционально увеличивается скорость сдвига:
τ=η0υ (41)
Выражение (41) представляет собой закон Ньютона, где τ – напряжение сдвига в Н/м2, υ -скорость сдвига в с-1, а η 0 –коэффициент пропорциональности между напряжением и скоростью сдвига, называемый коэффициентом вязкости или просто вязкостью и имеющий размерность Н·с/м2 (также пуаз).
Кривая 1 на рис.34 является, таким образом, простейшей кривой течения. Получить ее можно следующим образом. Представим себе некоторый объем жидкости, заключенный между двумя параллельными плоскостями (рис.35), например, каплю глицерина между стеклянными пластинками. Пусть на верхнюю пластинку действует сила F; тогда на каждый квадратный метр пластинки площадью A, м2 действует напряжение сдвига τ, Н/м2. Под действием напряжения сдвига пластинка сместится на расстояние ∆L. Интенсивность сдвига зависит, конечно, и от расстояния между пластинами. Если ∆L=1см, то при зазоре между пластинами L0=1м сдвиг вообще трудно заметить, а при зазоре L0=1мм деформация сдвига окажется огромной. Поэтому относительная деформация сдвига γ=∆L/L0, а скорость деформации сдвига υ=dγ/dt имеет размерность с-1, как отношение к единице времени безразмерной величины γ. Увеличивая напряжение сдвига и измеряя его скорость, можно построить кривую 1 рис. 34.
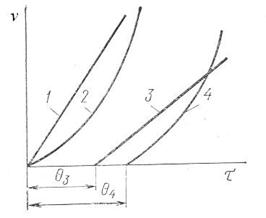 | 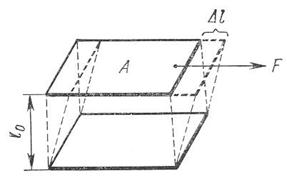 |
| Рис.34 Различные типы кривых течения (реологических кривых): зависимость скорости сдвига v от напряжения сдвига τ: 1 – для идеальной ньютоновской жидкости; 2 – для псевдопластической жидкости; 3 – для идеально пластичного тела; 4 – для неидеально пластичного тела; θ3, θ4 – пределы сдвига соответственно идеально и неидеально пластичного тела. | Рис.35 Схема деформации сдвига жидкости между плоскопараллельными пластинами. |
Такой тип кривой течения характерен для полимеров с узким молекулярно-массовым распределением и при переработке полимеров встречается сравнительно редко.
Обычно с ростом напряжения сдвига скорость течения растет быстрее, чем это следует из закона Ньютона (кривая 2, рис. 34). Полимеры, поведение которых в процессе течения описывается этой кривой, называются псевдопластичными жидкостями. Нетрудно сообразить, что ускорение течения, показанное кривой 2, обусловлено такими изменениями структуры полимера в процессе течения, которые приводят к падению вязкости. Чем больше напряжение сдвига, тем меньше вязкость (кривая 2, рис.35). Падение вязкости с ростом напряжения сдвига называют аномалией вязкости, а величину вязкости, зависящую от напряжения сдвига,- эффективной вязкостью.
Мы видим, что для большинства полимеров (растворов или расплавов) величина вязкости не может дать представления о реологических свойствах; в этих случаях необходимо получить полную кривую течения, т.е. зависимость вязкости (или скорости сдвига) от напряжения сдвига.
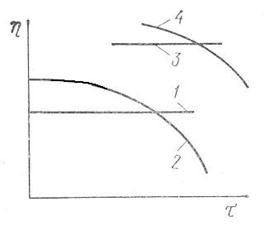 |
| Рис.35 Различные типы зависимости вязкости от напряжения сдвига полимеров, кривые течения которых приведены на рис......: 1 – ньютоновская жидкость; 2 – псевдопластичная жидкость; 3 – идеальное пластичное тело; 4 – реальное (неидеальное) пластичное тело. |
При введении наполнителя (особенно волокнистого) в полимеры частицы наполнителя образуют цепочечные структуры, соединяющиеся в пространственный каркас, обладающий значительной упругостью. При наложении напряжения сдвига такие системы сначала не текут, т. е. напряжение сдвига растет, а скорость течения остается нулевой, как это показано на рис. 34, кривые 3 и 4. Возникает некоторое предельное напряжение сдвига, после которого система течет либо как ньютоновская, либо как неньютоновская жидкость (соответственно кривые 3 и 4). Полимеры, течение в которых начинается при любом напряжении сдвига, называют вязкими; полимеры обладающие, предельным напряжением сдвига, ниже которого течение не возникает, называют пластичными.
 2014-02-02
2014-02-02 5492
5492
