Рассмотренные выше модели были построены в предположении конечной величины лага l. Предположим теперь, что для описания некоторого процесса используется модель с бесконечным лагом вида:
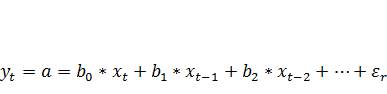 (7.16)
(7.16)
Очевидно, что параметры такой модели обычным МНК или с помощью иных стандартных статистических методов определить нельзя, поскольку модель включает бесконечное число факторных переменных. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т. е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической профессии. На рис. 7.1 геометрической структуре лага соответствует вариант 7.1 б).
Впервые изложенный в этом разделе подход к оценке параметров моделей с распределенным лагом типа (7.16) был предложен J1.M. Койком. Койк предположил, что существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b0 ед., то под воздействием изменения фактора, имевшего место в период (t — 1), результат изменится на b0 • λ ед.; в период (t - 2) — на b0 • λ • λ = b0 • λ2 ед., и т. д. Для некоторого периода (t — l) это изменение результата составит b0 • λ l ед. В более общем виде можно записать:
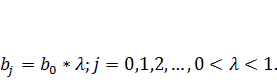 (7.17)
(7.17)
Ограничение на значения  > 0 обеспечивает одинаковые знаки для всех коэффициентов
> 0 обеспечивает одинаковые знаки для всех коэффициентов  > 0, а ограничение
> 0, а ограничение  < 1 означает, что с увеличением лага значения параметров модели (7.16) убывают в геометрической профессии. Чем ближе
< 1 означает, что с увеличением лага значения параметров модели (7.16) убывают в геометрической профессии. Чем ближе  к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора хt. Выразим с помощью (7.17) все коэффициенты bj в модели (7.16) через b0 и
к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора хt. Выразим с помощью (7.17) все коэффициенты bj в модели (7.16) через b0 и  :
:
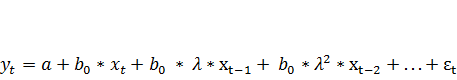 (7.18)
(7.18)
Тогда для периода (t — 1) модель (7.18) можно записать следующим образом:
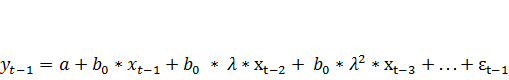 (7.19)
(7.19)
Умножим обе части модели (7.19) на  :
:
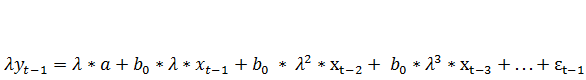 (7.20)
(7.20)
Вычтем найденное соотношение (7.20) из соотношения (7.18):
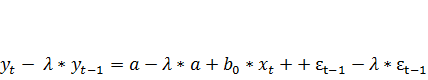
Преобразования (7.21) приводят нас к получению модели Койка:
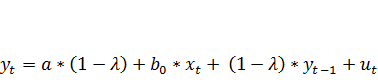 (7.22)
(7.22)
где 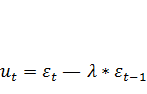
Полученная модель есть модель двухфакторной линейной регрессии (точнее — авторегрессии). Определив ее параметры, мы найдем  и оценки параметров а и b0 исходной модели. Далее с помощью соотношений (7.17) несложно определить параметры b1 b2,... модели (7.16). Отметим, что применение обычного МНК к оценке параметров модели (7.22) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной
и оценки параметров а и b0 исходной модели. Далее с помощью соотношений (7.17) несложно определить параметры b1 b2,... модели (7.16). Отметим, что применение обычного МНК к оценке параметров модели (7.22) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной  .
.
Описанный выше алгоритм получил название преобразования Койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные xt и yt-l. Несмотря на бесконечное число лаговых переменных в модели (7.16), геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели Койка. Поскольку сумма коэффициентов регрессии в модели (7.16) есть сумма геометрической профессии, т. е.
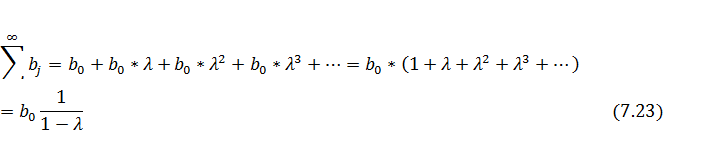
то средний лаг определяется как
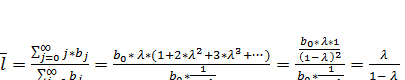 (7.24)
(7.24)
Нетрудно заметать, что при  = 0,5 средний лаг T = 1, а при l < 0,5 средний лаг
= 0,5 средний лаг T = 1, а при l < 0,5 средний лаг  < 1, т. е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 —
< 1, т. е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 —  ) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо выполнение следующего условия:
) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо выполнение следующего условия:
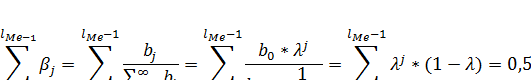
Поэтому медианный лаг в модели Койка равен (Если 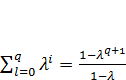 )
)
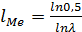 (7.26)
(7.26)
 2014-02-02
2014-02-02 2635
2635







