Й учебный вопрос. Метод Алмона

Рассмотрим общую модель с распределенным лагом, имею­щую конечную максимальную величину лага l, которая описыва­ется соотношением (7.3). Предположим, было установлено, что в исследуемой модели имеет место полиномиальная структура ла­га, т. е. зависимость коэффициентов регрессии b_i от величины ла­га описывается полиномом k-й степени. Частным случаем поли­номиальной структуры лага является линейная модель (рис. 7.1 а)). Примерами лагов, образующих полином 2-й степени, являются варианты рис. 7.1 г) и д). Перевернутая V-образная структу­ра лага также может быть аппроксимирована с помощью полино­ма 2-й степени. Наконец, график, представленный на рис. 7.1 е), является примером модели лагов в форме полинома 3-й степени. Лаги, структуру которых можно описать с помощью полиномов, называют также лагами Алмон, по имени Ш. Алмон, впервые об­ратившей внимание на такое представление лагов. Формально модель зависимости коэффициентов b_j от величи­ны лага j в форме полинома можно записать в следующем виде:

• для полинома 1-й степени: ;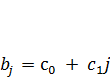

• для полинома 2-й степени: ;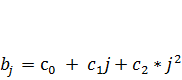

• для полинома 3-й степени: 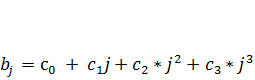; и т. д.

В наиболее общем виде для полинома k-й степени имеем.

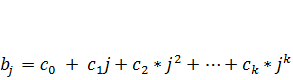
Тогда каждый из коэффициентов b_j модели (7.3) можно выра­зить следующим образом:

;

;

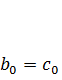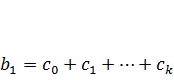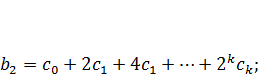
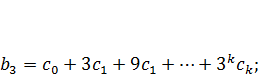
и т.д.

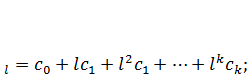(7.11)

Подставив в (7.3) найденные соотношения для получим:

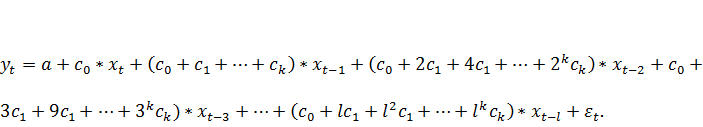; (7.12)

Перегруппируем слагаемые в (7.12)

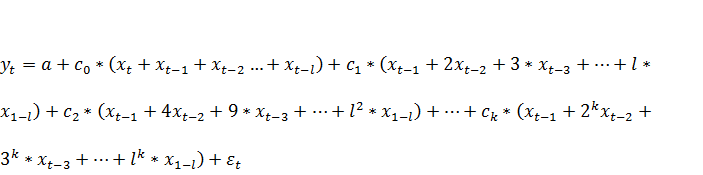(7.13)

Обозначим слагаемые в скобках при как новые перемен­ные:

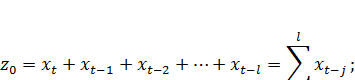
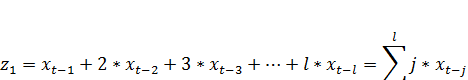
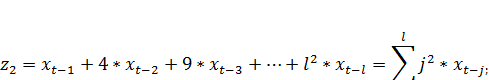
……………………………………………………………………… (7.14)

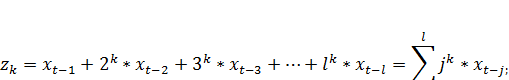
Перепишем модель (7.13) с учетом соотношений (7.14)

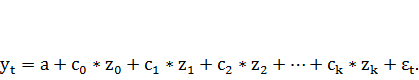(7.15)

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выглядит следующим образом.

1. Определяется максимальная величина лага l.

2. Определяется степень полинома k, описывающего структу­ру лага.

3. По соотношениям (7.14) рассчитываются значения пере­менных z₀…z_k

4. Определяются параметры уравнения линейной регрессии (7.15).

5. C помощью соотношений (7.11) рассчитываются парамет­ры исходной модели с распределенным лагом.

Применение метода Алмон сопряжено с рядом проблем.

Во-первых, величина лага l должна быть известна заранее. При ее определении лучше исходить из максимально возможного ла­га, чем ограничиваться лагами небольшой длины. Выбор мень­шего лага, чем его реальное значение, приведет к тому, что в мо­дели регрессии не будет учтен фактор, оказывающий значитель­ное влияние на результат, т. е. к неверной спецификации модели. Влияние этого фактора в такой модели будет выражено в остат­ках. Тем самым в модели не будут соблюдаться предпосылки МНК о случайности остатков, а полученные оценки ее параметров окажутся неэффективными и смещенными. Выбор большей величины лага по сравнению с ее реальным значением будет оз­начать включение в модель статистически незначимого фактора и снижение эффективности полученных оценок, однако эти оценки все же будут несмещенными.

Существует несколько практических подходов к определению реальной величины лага, например построение нескольких урав­нений регрессии и выбор наилучшего из этих уравнений или применение формальных критериев, например критерия Шварца. Однако наиболее простым способом является измерение тесноты связи между результатом и лаговыми значениями фактора. Кроме того, оптимальную величину лага можно приближенно опреде­лить на основе априорной информации экономической теории или проведенных ранее эмпирических исследований.

Во-вторых, необходимо установить степень полинома k. Обычно на практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя следующее простое правило: вы­бранная степень полинома k должна быть на единицу больше числа экстремумов в структуре лага. Если априорную информа­цию о структуре лага получить невозможно, величину k проще всего определить путем сравнения моделей, построенных для различных значений к, и выбора наилучшей модели.

В-третьих, переменные z, которые определяются как линей­ные комбинации исходных переменных х, будут коррелировать между собой в случаях, когда наблюдается высокая связь между самими исходными переменными. Поэтому оценку параметров модели (7.15) приходится проводить в условиях мультиколлинеарности факторов. Однако мультиколлинеарность факторов ,..., в модели (7.15) сказывается на оценках параметров b ₀,..., b_l в несколько меньшей степени, чем если бы эти оценки были полу­чены путем применения обычного МНК непосредственно к модели (7.3) в условиях мультиколлинеарности факторов 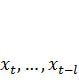. Это связано с тем, что в модели (7.15) мультиколлинеарность ве­дет к снижению эффективности оценок c ₀,..., c_k, поэтому каждый из параметров 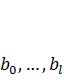которые определяются как линейные ком­бинации оценок 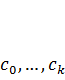будет представлять собой более точную оценку, а стандартные ошибки этих параметров не будут превы­шать стандартные ошибки параметров, полученных по модели (7.3) обычным МНК.

Метод Алмон имеет два неоспоримых преимущества. Он достаточно универсален и может быть применен для моде­лирования процессов, которые характеризуются разнообраз­ными структурами лагов. При относительно небольшом количестве переменных в (7.15) (обычно выбирают k = 2 или k = 3), которое не приво­дит к потере значительного числа степеней свободы, с помо­щью метода Алмон можно построить модели с распределен­ным лагом любой длины.