2014-02-02
2772
Дисперсия любой несмещенной оценки одного параметра θ удовлетворяет неравенству Рао-Крамера:
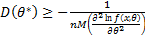(16.7)
где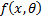 
– плотность распределения вероятностей случайной величины; 
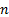– объем выборки.
Оценка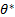 
, для которой в неравенстве Рао-Крамера достигается знак равенства, будет эффективной. В математической статистике применяются также асимптотически эффективные оценки, дисперсия которых стремится к нижней границе неравенства Рао-Крамера при 
.
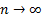Докажем с помощью неравенства (16.7), что выборочная средняя является эффективной оценкой для генеральной средней.
.
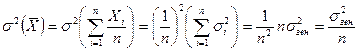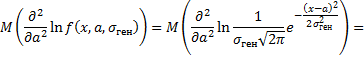
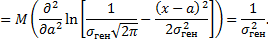
Подставляем найденное математическое ожидание в неравенство Рао-Крамера:
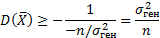
Таким образом, нижняя граница неравенства Рао-Крамера совпадает с дисперсией выборочной средней, что свидетельствует об эффективности выборочной средней.
