Показатели качества оценок

ОСНОВЫ ТЕОРИИ ТОЧЕЧНОГО ОЦЕНИВАНИЯ ПАРАМЕТРОВ

ЛЕКЦИЯ № 16

План

1. Показатели качества оценок

2. Неравенство Рао-Крамера

3. Метод максимального правдоподобия

Рассмотренные в лекции № 15 выборочные характеристики используются для оценки приближенных значений неизвестных числовых характеристик генеральной совокупности.

Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется её точечной статистической оценкой. «Точечная» означает, что оценка представляет собой число. «Статистическая» означает, что оценка рассчитывается по результатам наблюдений.

Выборочное среднее 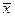– это точечная статистическая оценка генеральной средней 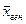(или математическое ожидание 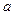); выборочная дисперсия 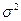– оценка генеральной дисперсии 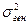. Обозначим через 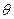некоторую генеральную характеристику (например, 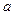и любая другая числовая характеристика случайной величины). Пусть 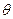^* – статистическая оценка неизвестного параметра 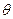теоретического распределения. Допустим, что по выборке объема найдена оценка . 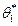Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по её данным найдем оценку 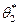. Повторяя опыт многократно, получим числа, которые, вообще говоря, различны между собой. Таким образом, оценку 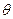^* можно рассматривать как случайную величину, а числа 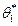, ,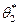…, 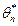– как её возможные значения.

Абсолютная разность 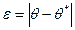называется ошибкой выборки.

Так как выборочная оценка является лишь некоторым приближением к параметру генеральной совокупности 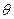, то желательно, чтобы ошибки оценивания была минимальной. Чтобы выбранная оценка была наилучшей, она должна обладать рядом свойств:

o состоятельностью;

o несмещенностью;

o эффективностью;

Определение 16.1. Оценка 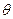^* генеральной характеристики 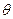называется состоятельной, если для любого 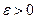выполняется равенство:

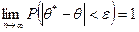(16.1)

Т. е. с ростом объема выборки вероятность того, что выборочная статистика 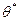приближается к оцениваемому параметру 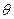возрастает.

Выполнение условия состоятельности гарантирует от грубых ошибок в оценке 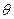при достаточно больших . Выборочная средняя – состоятельная оценка генеральной средней. Это происходит вследствие того, что средняя ошибка выборочной средней есть величина 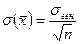. Когда объем выборки возрастает, то ошибка уменьшается, а вероятность того, что 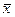будет ближе к математическому ожиданию, возрастает.

Определение 16.2. Оценка 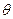^* генеральной характеристики 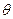называется несмещенной, если для любого фиксированного числа наблюдений выполняется условие – математическое ожидание оценки равно неизвестному параметру при любом объеме выборки:

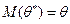(16.2)

Если математическое ожидание не равно оцениваемому параметру, то оценку называют смещенной. Смещение точечной оценки определяется как разность:

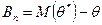(16.3)

Выборочная средняя является несмещенной оценкой генеральной средней, что было уже показано выше.

В качестве оценки генеральной дисперсии 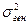используется выборочная дисперсия 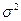. Однако эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия, как можно доказать, является смещенной оценкой. Другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно:

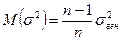(16.4)

Доказательство:

.

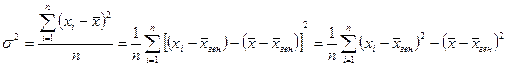
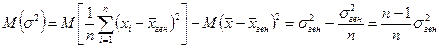Несмещенная оценка дисперсии называется исправленной дисперсией и вычисляется по формуле:

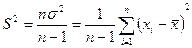(16.5)

Формула (16.5) отличается от обычной формулы для вычисления дисперсии только знаменателем. Если – велико, 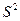практически совпадает со значением дисперсии, вычисленной обычным способом. При 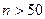между ними нет практически никакой разницы. Поэтому наряду с несмещенными оценками применяются асимптотически несмещенные оценки, для которых 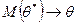при увеличении объема выборки.

Выборочная доля является несмещенной оценкой генеральной доли.

Определение 16.3. Статистическая оценка 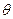^* характеристики 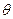называется эффективной, если она обладает наименьшей возможной дисперсией.

Степень эффективности оценивают отношением дисперсий:

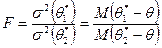(16.6)

Если 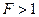, то оценка 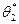более эффективна, чем .

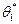Выборочная средняя 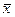при известном значении 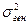является эффективной оценкой генеральной средней. Оценка выборочной дисперсии не обладает свойством эффективности, если неизвестны параметры нормального распределения, но если известно математическое ожидание 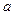, то выборочная дисперсия обладает свойством эффективности.