Алгоритм получения случайной величины, распределенной по Пуассону

12.10.2012

Модуль

/*

В основе моделирования сложных систем всегда лежит эксперимент: реальный или логический.

Суть реального эксперимента состоит в непосредственном изучении конкретной сложной системы. В ходе логического эксперимента свойства системы исследуются не на самой системе, а с помощью ее математического описания или содержательной словесной модели, которая изоморфна системе с точки зрения изучаемых в эксперименте свойств.

Подавай на вход системы различные входные процессы и измеряя процесс(ы) на выходе можно установить и записать математически существующую связь между ними в виде уравнения.

Кроме того, для адекватного отражения связи между входом и выходом системы в системотехнике вводится понятие состояния.

По своему смыслу состояние Z(τ) представляет собой совокупность существенных свойств (характеристик системы), знание кот в настоящем (в момент τ) позволяет определить ее поведение в будущем, когда t> τ.

Уравнение вход-выход имеет следующий вид:

Yt = A(T, z(τ),Xt) (1)

Где Yt и Xt – это входной и выходной процесс на интервале времени τ,

A – оператор выхода

Согласно (1) выходной процесс полностью определяется входным процессом и начальным состоянием и не зависит от того, каким образом система была переведена в это состояние.

Ур-е (1) ограничивает класс систем только теми системами, функционирование которых в настоящий момент не зависит от того, как они функционировали в прошлом.

Для полного описания процесса функционир-я системы зададим условие определения состояния системы. Для этого зададим понятие уравнения состояния:

z(t)=B(τt, z(τ), Xτt) (2)

B – оператор, который устанавливает однозначную зависимость z(t) от пары (z(τ), Xτt), которая задана на интервале τt и называется оператором перехода.

Уравнения (1) и (2) м логически обобщить для многомерной формы

.

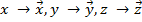Т.О. модель функционирования системы д обеспечивать прогнозирование процессов функционирования на всем интервале функционирования T (мн-во времени) по заданному вектору нач состояния 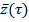, входному процессу .

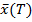Для решения задачи достаточно задать мн-во допустимых значений X и Y, возможных сост-й Z и операторов выхода А и перехода В, тогда модель функционирования системы без предыстории предст.собой процесс, который м.б. описан следующим кортежом:

MF=<T,X,Y,Z,A,B>. (3)

Если все эти компоненты известны, то модель функционирования этой системы полностью определена и может быть использована для описания и изучения свойственных системе процессов функционирования.

Множества и операторы, которые составляют общесистемную модель (3), могут обладать различными свойствами, совокупность которых позволяет конкретизировать хар-р функционирования системы:

N – непрерывность;

L – линейность;

S – стационарность;

P – стохастичность.

При построении модели функционирования систем применяют след.подходы:

1)непрерывно детерминированный подход (диф.уравнения);

2)дискретно детерминированный подход (конечные автоматы);

3)дискретно-стохастический подход (вероятностные автоматы);

4)непрерывно-стохастический подход (СМО);

5)обобщенный/универсальный подход (агрегативные системы);

*/

Согласно центральной предельной теореме теории вер-ти СВ 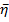распределена асимптотически нормально, если ε распределены одинаково.

Для практического получения значений η в качестве ε выбирают равномерно распределенные СВ. при этом наиболее часто используют преобразование:

,

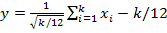Где xi- равномерно распределенные на (0, 1) случ.числа. при K=12 формула приобретает наиболее удобный для расчетов вид, но она дает достаточно точные рез-ты уже для K=3,4. Для получения y* распределенного нормально с произвольными m и σ, используются дополнительно с преобразованием:

y*=m+σy.

Закон Пуассона описывает число событий, происходящих за одинаковые промежутки времени, при условии независимости этих событий. Это распределение орошо описывает количество вызовов телефонной станции за определенное время суток, заказов такси и т.д. Закон Пуассона называют законом появления редких событий.

В основе алгоритма появления СЧ, распределенных по Пуассону, лежит теорема Пуассона. В соответствии с этой теоремой, если n – количество событий велико, а р – вер-ть успеха мала, то вер-ть того, что при n испытаниях событие произойдет k раз, равна:

,

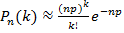np=a, а – параметр закона Пуассона.

Процедура получения чисел, распределенных по Пуассону, заключается в следующем:

1.положить р <=0,1 (т.к. события явл.редкими)

2.вычислить число испытаний n=a/p

3.значение х – случайного числа с равномерным на (0,1) законом распределения сравнить с р, если х<=p, то к счетчику событий добавляется 1.

4.проводится N испытаний, после чего содержимое счетчика можно считать случ.числом, распределенным по Пуассону.