ЛЕКЦИЯ №2
« ФОРМУЛА ТЕЙЛОРА »
 |
Формулы Тейлора и Маклорена.
Пусть функция 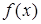 n раз дифференцируема в окрестности точки x0.Найдем многочлен
n раз дифференцируема в окрестности точки x0.Найдем многочлен 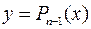 степени не выше n-1, такой что
степени не выше n-1, такой что
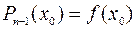 ,
, 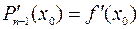 ,,…,
,,…, 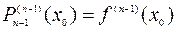 .
.
Такой многочлен в некотором смысле «близок» к функции 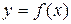 .
.
Будем искать этот многочлен в форме многочлена, разложенного по степеням  , с неопределенными коэффициентами:
, с неопределенными коэффициентами:
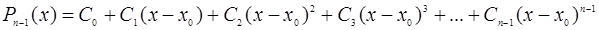 .
.
Неопределенные коэффициенты 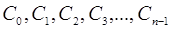 определим так, чтобы выполнялись перечисленные выше условия.
определим так, чтобы выполнялись перечисленные выше условия.
Найдем производные от  :
:
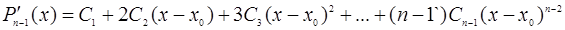 ;
;
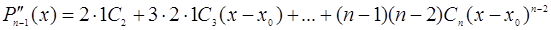 ;…
;…
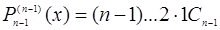 .
.
Подставляя 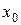 вместо
вместо  , находим:
, находим:
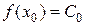 ,
, 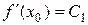 ,
, 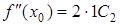 ,
, 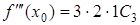 , …,
, …, 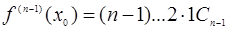 . Отсюда
. Отсюда
Þ 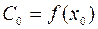 ,
, 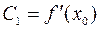 ,
, 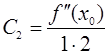 ,
, 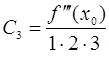 ,…,
,…, 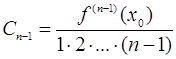 .
.
Искомый многочлен будет иметь вид:
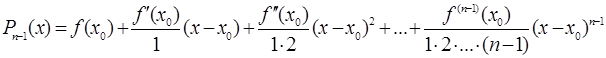 , или
, или
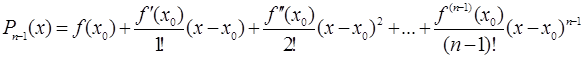 .
.
Этот многочлен мы будем называть многочленом Тейлора.
Оказывается, что справедлива следующая теорема:
Теорема. Пусть функция 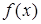 n раз дифференцируема в окрестности точки x0. Тогда в этой окрестности для функции
n раз дифференцируема в окрестности точки x0. Тогда в этой окрестности для функции 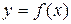 справедлива следующая формула Тейлора:
справедлива следующая формула Тейлора:
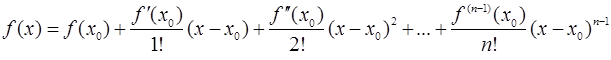 +
+
+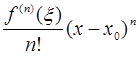 .
.
Здесь 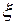 некоторая точка, заключенная между
некоторая точка, заключенная между 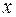 и
и 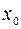 (
(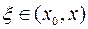 ), зависящая от
), зависящая от 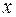 , а
, а 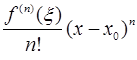 =
= 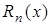 - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.
Доказательство: Обозначим через 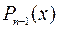 многочлен
многочлен
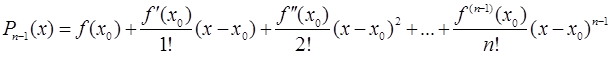 .
.
Ясно, что для каждого выбранного 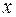 существует такое число
существует такое число  , для которого будет выполняться равенство:
, для которого будет выполняться равенство:
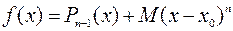 . (1)
. (1)
Покажем, что это число  при уже выбранном
при уже выбранном 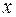 будет равно
будет равно 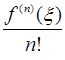 при некотором
при некотором 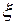 из промежутка
из промежутка 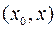 .
.
Определим функцию
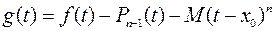 .
.
Ясно, что
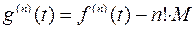
Следовательно, доказательство мы закончим, если покажем, что в некоторой точке 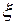 (
(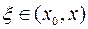 ) будет выполняться равенство:
) будет выполняться равенство: 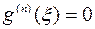 .
.
Непосредственными вычислениями проверяется (см. многочлен Тейлора!), что для всех 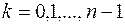 выполняются равенства:
выполняются равенства:
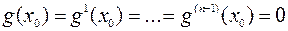 (2)
(2)
Число  выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно,
выбрано таким образом, чтобы выполнялось равенство (1) и, следовательно, 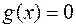 . Таким образом, для функции
. Таким образом, для функции 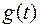 на промежутке
на промежутке
[ ] выполняются все условия теоремы Ролля. Следовательно, на интервале (
] выполняются все условия теоремы Ролля. Следовательно, на интервале ( ) существует такая точка
) существует такая точка 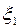 , производная функции
, производная функции 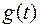 , в которой равна нулю, то есть
, в которой равна нулю, то есть 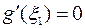 . Но тогда с учетом (2) теорему Ролля можно применить к функции
. Но тогда с учетом (2) теорему Ролля можно применить к функции 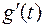 на промежутке [
на промежутке [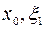 ] и так далее. Применяя, в конце концов, теорему Ролля к функции
] и так далее. Применяя, в конце концов, теорему Ролля к функции  на соответствующем промежутке, получим точку
на соответствующем промежутке, получим точку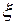 , для которой будет справедливо равенство
, для которой будет справедливо равенство 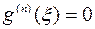 .
.
Утверждение доказано.
Если x0=0, то формула Тейлора превращается в формулу Маклорена:
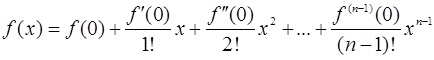 +
+ 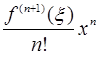
Заметим, что числа n могут выбираться различными, в зависимости и от наличия у функции производных соответствующего порядка, и от необходимой точности расчетов. Например, формула Тейлора для n=4 будет иметь вид:
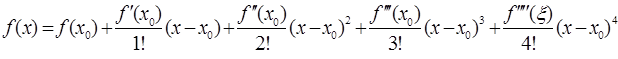
Разложение некоторых элементарных функций по формуле Маклорена.
1.  .
.
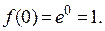
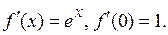
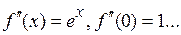
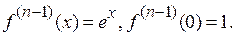
Þ 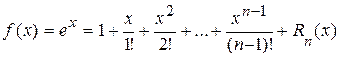 ,
,
где  .
.
2. 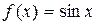 .
.

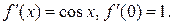
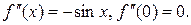
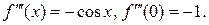
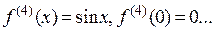
Þ 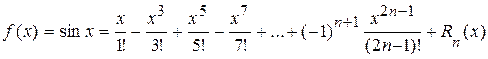 ,
,
где 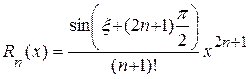 .
.
3. 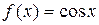 .
.
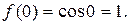
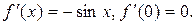

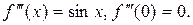
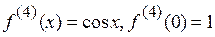 ,…
,…
Þ 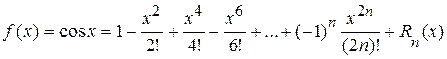 ,
,
где 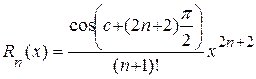 .
.
Пример:
Разложить функцию 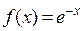 по формуле Маклорена, взяв 4 слагаемых.
по формуле Маклорена, взяв 4 слагаемых.
Воспользуемся формулой Маклорена для функции 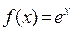 , заменив x на
, заменив x на
(-x):
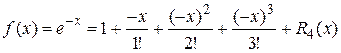 .
.
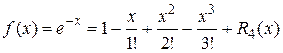 .
.
 2014-02-02
2014-02-02 189
189






