1. Рефлексивность. Отношение R называется рефлексивным, если (х, х)ÎR для любого хÎA. Примеры рефлексивных отношений: отношения "³", "£" на множестве R.
2. Антирефлексивность. Отношение R называется антирефлексивным, если (х, х)ÏR для любого хÎA. Примеры антирефлексивных отношений: отношения "<", ">" на множестве R.
Если R – антирефлексивное отношение, то xÏGR(x) и хÏHR(x) для любого хÎA.
3. Симметричность. Отношение R называется симметричным, если для любых x, yÎA из того, что (x, y)ÎR следует (y, x)ÎR и обратно. Примеры симметричных отношений: отношения "=" и "¹".
Если отношение R симметрично, то для любого хÎA
а) GR(x) = HR(x); б) R = R–1.
4. Антисимметричность. Отношение R называется антисимметричным, если для любых x и y из A из одновременного выполнения условий (x, y)ÎR и (y, x)ÎR следует, что x = y. Пример антисимметричного отношения. Пусть А – множество людей в данной очереди. Отношение R – "не стоять за кем-то в очереди" будет антисимметричным.
Пусть х = ВАСЯ, а y = ИВАНОВ. Тот факт, что (x, y)ÎR означает, что "ВАСЯ не стоит в очереди за ИВАНОВЫМ", (y, x)ÎR – "ИВАНОВ не стоит за ВАСЕЙ". Очевидно, что одновременное выполнение обоих включений может быть, только если ВАСЯ и есть ИВАНОВ, т.е. x = y.
Отношение "³" также антисимметрично: если x ³ y и y ³ x, то x = y.
5. Асимметричность. Отношение R асимметрично, если R Ç R-1= Æ, т.е. пересечение отношения R с обратным отношением пусто.
Эквивалентное определение асимметричности: из двух отношений (x, y) Î R и (y, x)ÎR одно не выполняется.
Примеры асимметричных отношений: ">", "<", "быть начальником".
Если R – асимметричное отношение, то из xRy следует y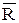 x.
x.
Для любого отношения R вводятся понятия симметричной части отношения Rs = R ÇR–1 и асимметричной части отношения Ra = R \ Rs. Если отношение R симметрично, то R= Rs, если отношение R асимметрично, то R = Ra.
Примеры. Если R – "³", то R–1 – "<", Rs – "=", Ra – ">".
6. Транзитивность. Отношение R транзитивно, если для любых x, y, zÎA из того, что (x, y)ÎR и (y, z)ÎR следует (x, z)ÎR.
Свойства транзитивного отношения:
а) RoR Í R;
б) для любого хÎA из yÎGR(x) следует, что GR(y) Í GR(x).
Не транзитивным является отношение "¹". Пусть x = 2, y = 3, z = 2, тогда справедливо x ¹ y и y ¹ z, но x = z, т.е. (x, z)ÏR.
Отношение R1 называется транзитивным относительно отношения R2, если:
а) из (x, y)Î R1 и (y, x)Î R2 следует, что (x, z)Î R1;
б) из (x, y)Î R2 и (y, x)Î R1 следует, что (x, z)Î R1.
7. Негатранзитивность. Отношение R называется негатранзитивным, если`R транзитивно.
Примеры. Отношения R1 –">" и R2 –" ¹" негатранзитивны, так как отношения`R1 – "£",`R2 – "=" транзитивны. Возможно одновременное выполнение свойств транзитивности и негатранзитивности. Например, отношение R1 одновременно транзитивно и негатранзитивно, а R2 , как известно, транзитивным не является.
8. Полнота. Отношение R полно, если для любых x, yÎА либо (x, y)ÎR, либо (y, x)ÎR, либо оба отношения выполняются одновременно.
Свойства полных отношений:
а) GR(x) È HR(x) = А для любого хÎA;
б) полное отношение рефлексивно.
9. Слабая полнота. Отношение R называется слабо полным, если для любых х ¹ y из А или (x, y)ÎR, или (y, x)ÎR.
Пример слабо полного отношения. Пусть А – множество предприятий, "неблагополучных" в смысле своего бюджета. Отношение R "быть должным" является слабо полным, так как каждое из этих предприятий или кому-либо должно, или ему кто-то должен, но быть должным самому себе нельзя и (x, x)ÏR.
10. Ацикличность. Бинарное отношение R ациклично, если Rn ÇR–1= Æ для любого nÎ N. Иными словами, если из любой конечной цепочки отношений х1Rx2, x2Rx3,..., xn-1Rxn следует, что x1 ¹ хn, то отношение R ациклично.
 2014-02-02
2014-02-02 4317
4317
