Граф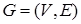ы, матрицы инцидентности и смежности

Граф состоит непустого множества 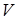(элементы которого называются вершинами, точками или узлами) и множества неупорядоченных пар различных элементов множества :

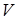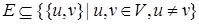
(элементы которого называются ребрами, линиями или дугами).

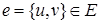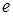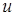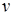Если , то говорят, что ребро соединяет вершины и . При этом вершины u и v называются концами ребра .

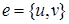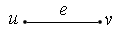
Диаграмма графа G =(V, E) представляется в виде точек (или кружков) на плоскости, каждая из которых изображает вершину графа. Ребро графа 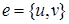изображается отрезком или дугой, соединяющей вершины u и v.

Диаграмму графа также называют графом.

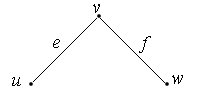
Две вершины графа u и v называются смежными, если они соединены некоторым ребром e графа. Вершина u и ребро e называются инцидентными, если u является концом ребра e. Два ребра e и f графа называются смежными, если они инцидентны одной и той вершине u графа.

(p, q)- граф – это граф с p вершинами и q ребрами

(p ³1 и ).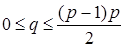

Тривиальный (p,0)-граф не содержит ни одного ребра.

Полный граф 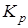– это 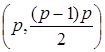-граф, содержащий все возможные ребра между 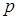вершинами.

Граф называется помеченным (или перенумерованным), если его точки обозначены попарно различными пометками.

Теорема. Существует 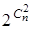помеченных графов с числом вершин n и 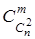помеченных (n, m)-графов.

Доказательство. Неупорядоченная пара { u, v } различных элементов u и v из множества V с числом элементов n есть сочетание без повторений из n элементов по 2. Поэтому число всех возможных ребер графа равно C_n ².

Каждый граф имеет множество ребер – некоторое подмножество множества из C_n ² элементов. Число всех подмножеств k -множества равно 2 ^k. Число всех 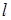-подмножеств k -множества равно .

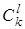Матрицей смежности графа называется матрица 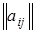, определяемая следующим образом: для всех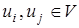

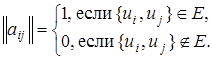
Матрицы смежности представляют собой квадратные матрицы с элементами 0 и 1, у которых по главной диагонали расположены нули. Матрица смежности графа симметрична относительно главной диагонали.

Матрицей инцидентности 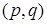-графа называется прямоугольная 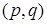-матрица , определяемая следующим образом: для всех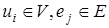

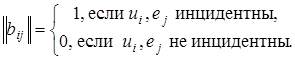
Примечание. Кроме графов (или неупорядоченных графов) рассматриваются и другие виды графов. Мультиграф отличается от графа тем, что две вершины могут быть соединены двумя и более ребрами. При этом ребра, соединяющие две вершины в количестве двух и более, называются кратными. Псевдограф отличается от графа тем, что в нем могут быть и кратные ребра, и петли (ребра, соединяющие вершины с самими собой). Ориентированный граф (или орграф) G =(V, E) отличается от графа тем, что E является множеством упорядоченных пар различных вершин множества V. На диаграмме две точки орграфа соединятся не линиями, а стрелками. В орграфах нет петель. Бинарное отношение 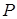графически представляются орграфом, в котором соотношение 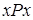изображается петлей, а соотношения 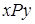и 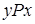двусторонней стрелкой (объединяются две противоположно направленные стрелки).