Линейное рекуррентное соотношение

Соотношение вида

a_{n + k} + p ₁ a_{n + k -1}+…+ p_ka_n = h (n) (2)

где h (n) – функция от числ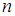а , а 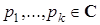, называется линейным рекуррентным соотношением.

Линейное рекуррентное соотношение называют однородным, если f (n)=0:

a_{n + k} + p ₁ a_{n + k -1}+…+ p_ka_n =0. (3)

Многочлен x^k + p ₁ x^{k -1}+…+ p_{k -1} x + p_k называется характеристическим для соотношения (2).

Корень a многочлена 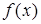называется простым, если 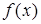делится на 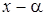, но не делится на .

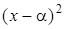Корень a многочлена 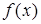называется кратным, если 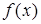делится на 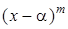, но не делится на , .

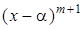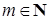При этом число 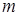называется кратностью корня .

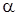Основная теорема алгебры: многочлен степени 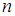с комплексными коэффициентами имеет 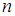комплексных корней с учетом их кратности.

Теорема 1. Пусть характеристический многочлен однородного линейного рекуррентного соотношения (3) имеет n простых корней a₁, …, a _n. Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:

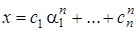, (4)

где c ₁,…, c_k Î C.

Доказательство. Легко проверить следующие два утверждения.

(a) Последовательность cxⁿ, где c Î C, является решением рекуррентного соотношения (3).

(b) Если последовательности a_n и b_n являются решениями соотношения (3), то последовательность a_n + b_n также является решением соотношения (3).

Из (a) и (b) следует, что любая последовательность вида (4) является решением соотношения (3).

Обратно, любое решение соотношения (3) имеет вид (4).

При n =0,1,…, k -1, из равенства (4) мы получим систему линейных уравнений относительно c ₁,…, c_k:

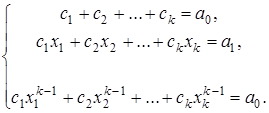(5)

Определитель системы (5) есть известный в алгебре определитель Вандермонда:

.

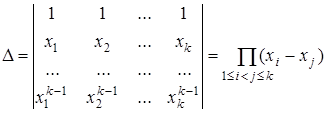Так как простые корни x ₁,…, x_k попарно различные, то D¹0. Значит, система (5) имеет (единственное) решение.

Теорема 2. Пусть характеристический многочлен однородного линейного рекуррентного соотношения (3) имеет k корней: a₁ кратности 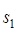, …, a _k кратности 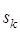, , 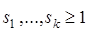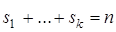. Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:

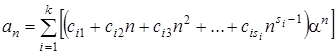, (6)

где .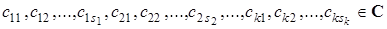

Замечание. Общее решение неоднородного линейного соотношения (2) можно найти как сумму общего решения однородного линейного соотношения (3) и частного решения неоднородного линейного соотношения (2).