Предел последовательности

Определение 1. Последовательность 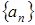называется сходящейся, если существует предельное значение 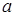, к которому стремятся ее элементы при 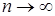, другими словами, если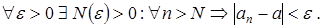

Число 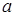называется пределом последовательности, при этом вводится обозначение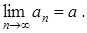

Определение 2. Последовательность называется расходящейся, если предела не существует или он равен бесконечности.

Примеры.

1. Элементы последовательности 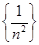уменьшаются с ростом 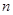, оставаясь положительными. Ясно, что ее предельное значение равно нулю.

Итак, 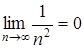. Покажем, что для каждого 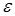можно определить номер N, начиная с которого выполняется условие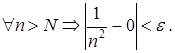

Пусть 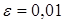. Из определения предела следует, что

.

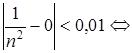
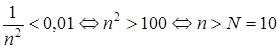Пусть 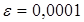, тогда

.

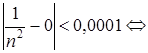
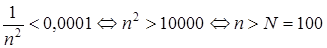2. Покажем, что для последовательности 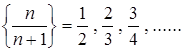предельное значение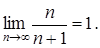

Из определения предела следует, что

.

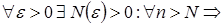
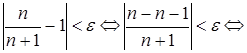
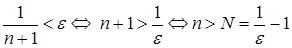Например, при .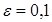

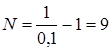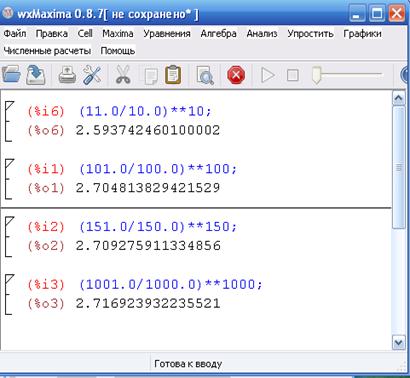3. Последовательность 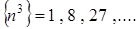возрастает с ростом 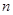, стремясь к бесконечности. Последовательность расходящаяся .

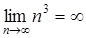4. Последовательность 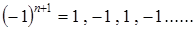не имеет предельного значения и также расходящаяся.

5. Последовательность

имеет предельное значени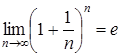е, где

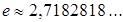- неперовое число.

Определение 3. Последовательность называется бесконечно малой, если ее предельное значение равно нулю.

Определение 4. Последовательность называется бесконечно большой, если ее предельное значение равно бесконечности.

Определение 5. Последовательность 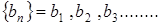называется подпоследовательностью последовательности 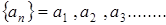, если все ее элементы являются элементами последовательности .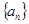

К примеру, последовательность 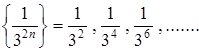является подпоследовательностью последовательности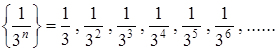

Доказана теорема, что если последовательность сходится к некоторому значению, то все ее подпоследовательности сходятся и к тому же значению.