1. Первый замечательный предел 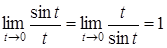 .
.
Доказательство: Возьмем круг радиуса 1, обозначим радиальную меру угла MOB через t. Функция 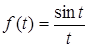 четная, т.к.
четная, т.к.
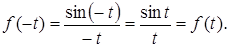
По условию 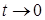 и отношение
и отношение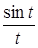 положительно при любом знаке t, следовательно, достаточно рассмотреть значения t, удовлетворяющие неравенствам
положительно при любом знаке t, следовательно, достаточно рассмотреть значения t, удовлетворяющие неравенствам  .
.
Очевидно, что
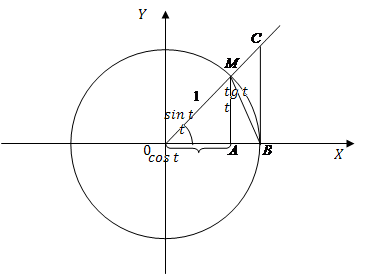
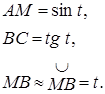
Рассмотрим треугольники 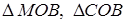 и сектор
и сектор 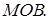 Очевидно имеем
Очевидно имеем
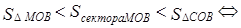
 .
.
Поделим все на  , тогда
, тогда

Так как, 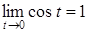 и
и 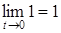 , то по принципу двух милиционеров
, то по принципу двух милиционеров 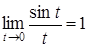 .
.
2. Второй замечательный предел (без вывода)
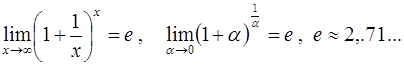
 2014-02-02
2014-02-02 474
474








