Непрерывность функции. Определение 1. Пусть функция определена в точке a и в некоторой окрестности этой точки

Определение 1. Пусть функция 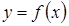определена в точке a и в некоторой окрестности этой точки. Функция 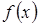называется непрерывной в точке 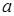, если .

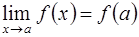Определение 2. Функция 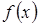непрерывна в точке 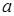, если .

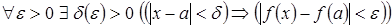Замечание. Эти определения эквивалентны, поскольку опираются на два эквивалентные определения предела.

Определение 3. Функция 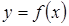непрерывна в точке 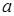, если 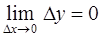, где 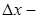приращение аргумента функции 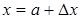, а 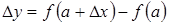- есть приращение функции, соответствующее приращению ее аргумента .

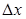Доказательство следует из первого определения непрерывной функции

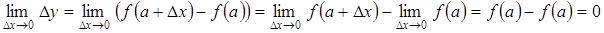, здесь первый из пределов вычисляется с помощью определения 1, второй – как предел постоянной, поскольку 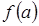не зависит от .

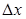Определение 4. Функция 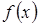непрерывна в точке 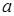, если

.

Определение 5. Функция 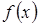непрерывна в некоторой области, если она непрерывна во всех точках этой области.

Свойства непрерывных функций

1) Сумма непрерывных функций – есть непрерывная функция.

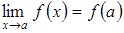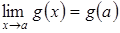Если и , то

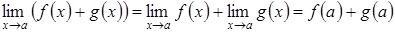. Доказано.

2) Произведение непрерывных функций есть функция непрерывная.

3) Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.

Доказательства второго и третьего свойств также следует из свойств пределов.

4) Пусть функция 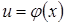непрерывна в точке 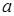, а другая функция 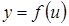непрерывна в точке 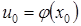. Тогда сложная функция 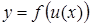непрерывна в точке a.

Пример. Функция 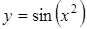непрерывна во всех точках числовой оси, так как и , и 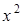непрерывны в этой области.