Лекция 5
1) Предел постоянной равен самой постоянной. Это свойство следует из первого определения предела.
2) Постоянную можно выносить за знак предела.
В самом деле, пусть 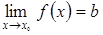 , в соответствии с теоремой
, в соответствии с теоремой 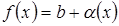 , причем
, причем 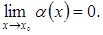 Очевидно,
Очевидно, 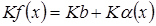 , где
, где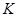 постоянная, но
постоянная, но 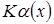 - бесконечно малая при
- бесконечно малая при 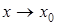 , что следует из свойств бесконечно малых, тогда функция
, что следует из свойств бесконечно малых, тогда функция 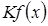 отличается от
отличается от 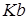 , следовательно,
, следовательно, 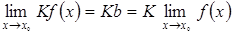 .
.
3) Предел суммы двух функций равен сумме пределов этих функций, если
они существуют.
Пусть 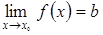 и
и 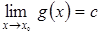 , тогда
, тогда 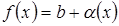 и
и 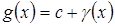 , где
, где  и
и 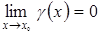 , тогда
, тогда  . Но подчеркнутые члены – есть бесконечно малая, и
. Но подчеркнутые члены – есть бесконечно малая, и
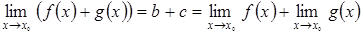 .
.
4) Предел произведения двух функций равен произведению их пределов,
если они существуют (доказывается аналогично).
5) 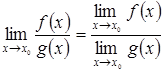 , если оба предела существуют и
, если оба предела существуют и 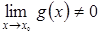 .
.
6) Если  , то
, то 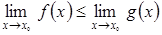 .
.
7) Принцип двух милиционеров.
Если 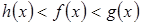 и
и  , то
, то 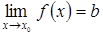 .
.
 2014-02-02
2014-02-02 254
254







