2014-02-02
659
Лекция 8
Определение 4. Функция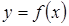 
называется выпуклой на интервале
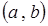, если точки касательных к функции на этом интервале расположены выше точек функции.
Определение 5. Функция 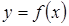называется вогнутой на интервале
, если точки касательных к функции на этом интервале расположены ниже точек функции.
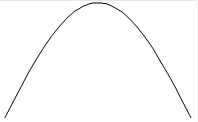
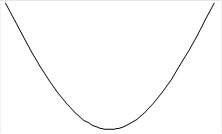
Выпуклая функция Вогнутая функция
Определение 6. Точки, в которых выпуклость переходит в вогнутость, или наоборот, называются точками перегиба функции.
Теорема. Необходимым условием точки перегиба является равенство нулю в ней второй производной.
Теорема. Достаточным условием выпуклости функции 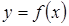на интервале 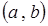является 
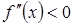. Достаточным условием вогнутости функции 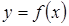на интервале является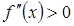 
.
Для доказательства теоремы запишем уравнение касательной к кривой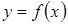 
в точке 
: 
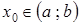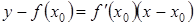. Вспомним также формулу Тейлора, которую представим следующим образом
.
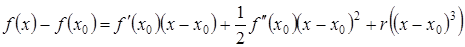Вычитаем эту формулу из формулы касательной, тогда
,
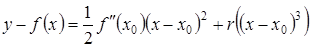где 
ординаты точек касательной. Знак правой части определяется первым ее членом, поскольку остаточный член 
в окрестности 
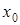мал по сравнению с основным членом, таким образом. При условии 
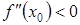разность между значением касательной и функции отрицательна, следовательно, точки касательной лежат выше точек кривой, и функция выпуклая. Перебирая различные точки 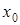интервала 
, убеждаемся, что первая часть теоремы доказана. Аналогично доказывается вогнутость кривой.
Теорема. Если 
и при переходе через нее вторая производная меняет знак, эта точка – точка перегиба.
Пример.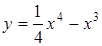 
. 
.
, 
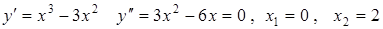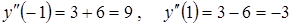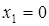точка перегиба, в которой вогнутость переходит в выпуклость,
, 
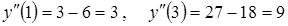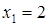не точка перегиба.
