Статистические решения для одного диагностического параметра

СТАТИСТИЧЕСКИЕ РЕШЕНИЯ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ И ДРУГИЕ ОБОБЩЕНИЯ

СТАТИСТИЧЕСКИЕ РЕШЕНИЯ ДЛЯ ОДНОГО ДИАГНОСТИЧЕСКОГО ПАРАМЕТРА

План лекции

Анализ и проверка домашней работы

Организационный момент.

Ход лекции.

Лекция 9

Тема. МЕТОДЫ СТАТИСТИЧЕСКИХ РЕШЕНИЙ

Цель. Дать понятие о статистических решениях для одного диагностического параметра и для принятия решения при наличии зоны неопределенности.

1. Учебная. Разъяснить процесс принятия решения в различных ситуациях.

2. Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.

3. Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

· Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.

· Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

1. Методическая разработка к занятию.

2. Учебный план.

3. Учебная программа

4. Рабочая программа.

5. Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

· Рабочие тетради

3. Ответьте на вопросы:

1. Что позволяет определить формула Байеса?

2. В чем состоят основы метода Байеса? Приведите формулу. Дайте определение точного смысла всех входящих в эту формулу величин.

3. Что означает, что реализация некоторого комплекса признаков K* яв­ляется детерминирующей?

4. Объясните принцип формирования диагностической матрицы.

5. Что означает решающее правило принятия?

6. Дайте определение методу последовательного анализа.

7. В чем состоит связь границ принятия решения с вероятностями ошибок пер­вого и второго рода?

Рассматриваемые методы относятся к статистическим. В методах статистических решений решающее правило выбирается исходя из некоторых условий оптимальности, например из условия мини­мума риска. Возникшие в математической статистике как методы проверки статистических гипотез (работы Неймана и Пирсона), рассматриваемые методы нашли широкое применение в радио­локации (обнаружение сигналов на фоне помех), радиотехнике, общей теории связи и других областях. Методы статистических решений успешно используются в задачах технической диагно­стики.

Если состояние системы характеризуется одним пара­метром, то система имеет одномерное пространство признаков. Разделение производится на два класса (дифференциальная диаг­ностика или дихотомия (раздвоенность, последовательное деление на две части, не связанные между собой.)).

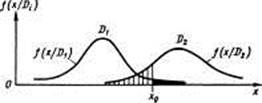
Рис.1 Статистические рас­пределения плотности веро­ятности диагностического па­раметра х для исправного D₁ и дефектного D₂ со­стояний

Существенно, что области исправного D₁ и дефектного D₂ состояний пересекаются и потому принципиально невозможно выбрать значение х₀, при котором не было бы ошибочных решений. Задача состоит в том, чтобы выбор х₀ был в некотором смысле оптимальным, например давал наименьшее число ошибочных решений.

Ложная тревога и пропуск цели (дефекта). Эти встречавшиеся ранее термины явно связаны с радиолокационной техникой, но они легко интерпретируются в задачах диагностики.

Ложной тревогой называется случай, когда принимается ре­шение о наличии дефекта, но в действительности система нахо­дится в исправном состоянии (вместо D₁ принимается D₂).

Пропуск цели (дефекта) — принятие решения об исправном состоянии, тогда как система содержит дефект (вместо D₂ при­нимается D₁).

В теории контроля эти ошибки называются риском постав­щика и риском заказчика. Очевидно, что эти двоякого рода ошибки могут иметь различные последствия или различные целы.

Вероятность ложной тревоги равна вероятности произведения двух событий: наличие исправного состояния и значения х > х₀.

Средний риск. Вероятность принятия ошибочного решения сла­гается из вероятностей ложной тревоги и пропуска дефекта (математическое ожидание) риска.

Разумеется, цена ошибки имеет условное значение, но она должна учесть предполагаемые последствия ложной тревоги и пропуска дефекта. В задачах надежности стоимость пропуска дефекта обычно существенно больше стоимости ложной тревоги.

Метод минимального риска. Вероятность принятия ошибочного решения определяется как минимизация точки экстремума среднего риска ошибоч­ных решений при максимуме правдоподобия т.е. проводится расчет минимального риска происхождения события при налички информации о максимально подобных событиях.

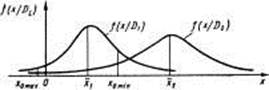
рис. 2. Точки экстремума среднего риска ошибоч­ных решений

Рис. 3. Точки экстремума для двугорбых распределе­ний

Отношение плотностей вероятно­стей распределения х при двух состояниях называется отноше­нием правдоподобия.

Напомним, что диагноз D₁ соответствует исправному состоянию, D₂ — дефектному состоя­нию объекта; С₂₁ — цена ложной тревоги, С₁₂ — цена пропуска цели (первые индекс — принятое состояние, второй — действи­тельное); С₁₁ < 0, С₂₂ < 0 — цены правильных решений (ус­ловные выигрыши). В большинстве практических задач условные выигрыши (поощрения) для правильных решений не вводятся.

Часто оказывается удобным рассматривать не отношение правдоподобия, а логарифм этого отношения. Это не изменяет результата, так как логарифмическая функция возрастает моно­тонно вместе со своим аргументом. Расчет для нормального и некоторых других распределений при использовании логарифма отношения правдоподобия оказывается несколько проще. Условие минимума риска можно получить из других соображений, которые окажутся важными в дальнейшем.

Метод минимального числа ошибочных решений.

Вероятность ошибочного решения для решающего правила

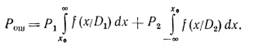
В задачах надежности рассматриваемый метод часто дает «неосторожные решения», так как последствия ошибочных реше­ний существенно различаются между собой. Обычно цена про­пуска дефекта существенно выше цены ложной тревоги. Если указанные стоимости приблизительно одинаковы (для дефектов с ограниченными последствиями, для некоторых задач контроля и др.) то применение метода вполне оправдано.

Метод минимакса предназначен для ситуации, когда отсут­ствуют предварительные статистические сведения о вероятности диагнозов D₁ и D₂. Рассматривается «наихудший случай», т. е. наименее благоприятные значения Р₁ и Р₂, приводящие к наи­большему значению (максимуму) риска.

Можно показать для одномодальных распределений, что вели­чина риска становится минимаксной (т. е. минимальной среди максимальных значений, вызванных «неблагоприятной» величи­ной Pi). Отметим, что при Р₁ = 0 и Р₁ = 1 риск принятия оши­бочного решения отсутствует, так как ситуация не имеет неопре­деленности. При Р₁ = 0 (все изделия неисправны) вытекает х₀ → -оо и все объекты действительно признаются неисправными; при Р₁ = 1 и Р₂ = 0 х₀ → +оо и в соответствии с имеющейся ситуацией все объекты классифицируются как исправные.

Для промежуточных значений 0 < Pi < 1 риск возрастает и при P1= P1* становится максимальным. Рассматриваемым методом выбирают величину х₀ таким образом, чтобы при наименее благоприятных значениях Pi потери, связанные с ошибочными решениями, были бы минимальными.

рис. 4. Определение гра­ничного значения диагно­стического параметра по методу минимакса

Метод Неймана—Пирсона. Как уже указывалось, оценки стои­мости ошибок часто неизвестны и их достоверное определение связано с большими трудностями. Вместе с тем ясно, что во всех случаях желательно при определенном (допустимом) уровне одной из ошибок минимизировать значение другой. Здесь центр проб­лемы переносится на обоснованный выбор допустимого уровня ошибок с помощью предыдущего опыта или интуитивных сооб­ражений.

По методу Неймана—Пирсона минимизируется вероятность пропуска цели при заданном допустимом уровне вероятности ложной тревоги. Таким образом, вероятность ложной тревоги

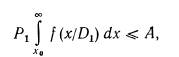
где А — заданный допустимый уровень вероятности ложной тревоги; Р₁ — вероятность исправного состояния.

Отметим, что обычно это условие относят к условной ве­роятности ложной тревоги (множитель Р₁ отсутствует). В задачах технической диагностики значения Р₁ и Р₂ в большинстве слу­чаев известны по статистическим данным.

Таблица 1 Пример - Результаты расчета по методам статистических решений

№ п/п	Метод	Гранич­ное зна­чение	Вероят­ность ложной тревоги	Вероят­ность пропуска дефекта	Средний риск
	Метод минимального риска	7,46	0,0984	0,0065	0,229
	Метод минимального числа ошибок	9,79	0,0074	0,0229	0,467
	Метод минимакса	Основной вариант	5,71	0,3235	0,0018	0,360
	2 вариант	7,80	0,0727	0,0081	0,234
	Метод Неймана—Пирсона	7,44	0,1000	0,0064	0,230
	Метод наибольшего прав­доподобия	8,14	0,0524	0,0098	0,249

Из сопоставления видно, что метод минимального числа ошибок дает неприемле­мое решение, так как цены ошибок существенно различны. Граничное значение по этому методу приводит к значительной вероятности пропуска дефекта. Метод минимакса в основном варианте требует очень большого снятия с эксплуатации исследуемых устройств(примерно 32%), так как исходит из наименее благоприят­ного случая (вероятность неисправного состояния Р₂ = 0,39). Применение ме­тода может быть оправданным, если отсутствуют даже косвенные оценки вероят­ности неисправного состояния. В рассматриваемом примере удовлетворительные результаты получаются по методу минимального риска.