Правило решения при наличии зоны неопределенности

СТАТИСТИЧЕСКИЕ РЕШЕНИЯ ПРИ НАЛИЧИИ ЗОНЫ НЕОПРЕДЕЛЕННОСТИ И ДРУГИЕ ОБОБЩЕНИЯ

В неко­торых случаях, когда требуется высокая надежность распозна­вания (большая стоимость ошибок пропуска цели и ложной тре­воги), целесообразно ввести зону неопределенности (зону отказа от распознавания). Правило решения будет следующим

при 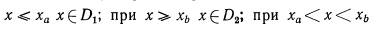отказ от распознавания.

Разумеется, отказ от распознавания является нежелательным событием. Он свидетельствует, что имеющейся информации недо­статочно для принятия решения и нужны дополнительные све­дения.

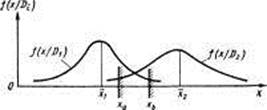
рис. 5. Статистические решения при наличии зоны неопределенности

Определение среднего риска. Величина среднего риска при наличии зоны отказа от распознавания может быть выражена следующим равенством

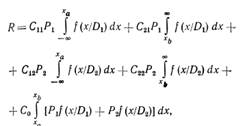
где C_o — цена отказа от распознавания.

Отметим, что С_о > 0, иначе задача теряет смысл («вознаграж­дение» за отказ от распознавания). Точно так же С₁₁ < 0, С₂₂ < 0, так как правильные решения не должны «штрафоваться».

Метод минимального риска при наличии зоны неопределенно­сти. Определим границы области принятия решения, исходя из минимума среднего риска.

Если не поощрять правильные решения (С₁₁ = 0, С₂₂ = 0) и не платить за отказ от распознавания (С₀ = 0), то область неопределенности будет занимать всю область изменения параметра.

Наличие зоны неопределенности дает возможность обеспе­чить заданные уровни ошибок за счет отказа от распознавания в «сомнительных» случаях

Статистические решения для нескольких состояний. Выше были рассмотрены случаи, когда статистические решения принимались для различения двух состояний (дихотомия). Принципиально такая процедура позволяет провести разделение на n состояний, каждый раз объединяя результаты для состояния D₁ и D₂. Здесь под D₁ понимаются любые состояния, соответствующие условию «не D₂». Однако в некоторых случаях представляет интерес рас­смотреть вопрос и в прямой постановке — статистические реше­ния для классификации n состояний.

Выше рассматривались случаи, когда состояние системы (изделия) характеризовалось одним параметром х и соответствующим (од­номерным) распределением. Состояние системы характеризуется диагностическими параметрами х₁ х₂,..., х_n или вектором х:

х=(х₁ х₂,...,х_n).