План
Темы: Выбор в условиях неопределенности.
Примерный план лекции №12 и основные определения.
- Выбор в условиях неопределенности: лотереи, отношение к риску, функция ожидаемой полезности, денежный (гарантированный) эквивалент лотереи.
- Приложения теории ожидаемой полезности: модель формирования портфеля инвестиций.
- Модель с контингентными благами.
Основные определения и утверждения
Пусть 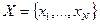 - множество возможных исходов. Простой лотереей будем называть набор вероятностей
- множество возможных исходов. Простой лотереей будем называть набор вероятностей 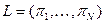 , где
, где 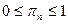 – вероятность исхода
– вероятность исхода 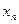 и
и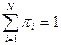 . Обозначим множество простых лотерей через
. Обозначим множество простых лотерей через 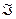 .
.
Определение. Предпочтения потребителя представимы функцией ожидаемой полезности, если каждому исходу 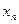 можно присвоить число
можно присвоить число 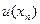 таким образом, что для любых двух лотерей
таким образом, что для любых двух лотерей 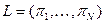 и
и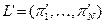 :
: 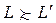 равносильно
равносильно 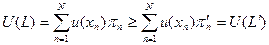 .
.
Функция U называется функцией ожидаемой полезности или функцией полезности Неймана-Моргенштерна (von Neumann-Morgenstern).
Функцию 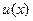 принято называть элементарной функцией полезности или функцией полезности Бернулли (будем считать ее непрерывной и возрастающей).
принято называть элементарной функцией полезности или функцией полезности Бернулли (будем считать ее непрерывной и возрастающей).
Утверждение (Единственность функции ожидаемой полезности).Если функция 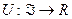 – функция ожидаемой полезности, представляющая предпочтения, определенные на
– функция ожидаемой полезности, представляющая предпочтения, определенные на 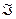 , то
, то 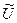 - другая функция ожидаемой полезности, отражающая те же предпочтения на
- другая функция ожидаемой полезности, отражающая те же предпочтения на 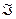 тогда и только тогда, когда существуют числа
тогда и только тогда, когда существуют числа 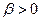 и
и 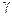 такие, что
такие, что  для любой лотереи
для любой лотереи 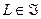 .
.
Определение. Будем говорить, что индивид не склонен к риску, если любая лотерея 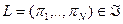 для него не лучше ожидаемого выигрыша этой лотереи,
для него не лучше ожидаемого выигрыша этой лотереи, 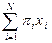 , полученного с определенностью. Если потребитель строго предпочитает ожидаемый выигрыш самой лотерее, то говорят, что он строго не склонен к риску или рискофоб.
, полученного с определенностью. Если потребитель строго предпочитает ожидаемый выигрыш самой лотерее, то говорят, что он строго не склонен к риску или рискофоб.
Будем говорить, что индивид нейтрален к риску, если он безразличен между лотереей и ее ожидаемым выигрышем, полученным с определенностью.
Будем говорить, что индивид склонен к риску, если предпочитает лотерею ее ожидаемому выигрышу, полученному с определенностью. Если потребитель строго предпочитает лотерею ее ожидаемому выигрышу, то говорят, что он строго склонен к риску или рискофил.
Если предпочтения индивида представимы с помощью функции ожидаемой полезности, то несклонность к риску означает вогнутость элементарной функции полезности 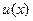 (для рискофоба – строгую вогнутость); склонность к риску эквивалентна выпуклости элементарной функции полезности
(для рискофоба – строгую вогнутость); склонность к риску эквивалентна выпуклости элементарной функции полезности 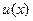 (для рискофила – строгой выпуклости); у нейтрального к риску индивида элементарная функция полезности линейна.
(для рискофила – строгой выпуклости); у нейтрального к риску индивида элементарная функция полезности линейна.
Определение. Денежным (гарантированным) эквивалентом лотереи 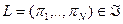 будем называть сумму денег
будем называть сумму денег 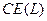 (полученную с определенностью), которая приносит индивиду такую же полезность, что и данная лотерея:
(полученную с определенностью), которая приносит индивиду такую же полезность, что и данная лотерея: 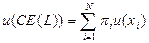 .
.
Задача формирования оптимального портфеля инвестиций (из двух активов: рискового и безрискового). Пусть индивид решает, как ему распределить свое богатство  между двумя активами. Первый актив – безрисковый: вложив 1 рубль в этот актив, он получит рубль обратно без какого-либо дополнительного дохода. Вложив 1 рубль во второй актив, можно получить
между двумя активами. Первый актив – безрисковый: вложив 1 рубль в этот актив, он получит рубль обратно без какого-либо дополнительного дохода. Вложив 1 рубль во второй актив, можно получить 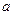 с вероятностью
с вероятностью 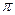 и
и 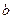 с вероятностью
с вероятностью 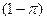 , где
, где 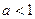 ,
, 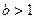 ,
, 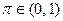 . Будем считать, что предпочтения потребителя представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности. Тогда для индивида-рискофоба условие
. Будем считать, что предпочтения потребителя представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности. Тогда для индивида-рискофоба условие 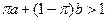 является необходимым и достаточным условием положительного спроса на рисковый актив.
является необходимым и достаточным условием положительного спроса на рисковый актив.
Определение. Назовем контингентным благ ом 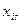 право (контракт) на получение
право (контракт) на получение  -го физического блага в количестве
-го физического блага в количестве 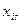 в случае реализации состояния природы
в случае реализации состояния природы 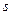 .
.
 2014-02-02
2014-02-02 320
320







