План
Темы: Выбор в условиях неопределенности.
Примерный план лекции №13 и основные определения.
- Модель формирования портфеля инвестиций: задача, условия первого порядка, необходимое и достаточное условие положительного спроса на рисковый актив; сравнительная статика.
- Модель с контингентными благами: определение контингентных благ; предпочтения на множестве контингентных благ; бюджетное ограничение в терминах контингентных благ; графическая иллюстрация.
Основные определения и утверждения
Модель формирования оптимального портфеля инвестиций (из двух активов: рискового и безрискового). Пусть индивид решает, как ему распределить свое богатство 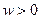 между двумя активами. Первый актив – безрисковый: вложив 1 руб. в этот актив, он получит
между двумя активами. Первый актив – безрисковый: вложив 1 руб. в этот актив, он получит 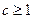 руб. обратно без какого-либо дополнительного дохода. Вложив 1 руб. во второй актив, рисковый, можно получить
руб. обратно без какого-либо дополнительного дохода. Вложив 1 руб. во второй актив, рисковый, можно получить 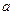 с вероятностью
с вероятностью 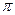 и
и 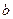 с вероятностью
с вероятностью 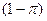 , где
, где 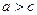 ,
, 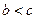 ,
, 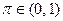 . Будем считать, что предпочтения потребителя представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности. Пусть
. Будем считать, что предпочтения потребителя представимы функцией ожидаемой полезности с дифференцируемой элементарной функцией полезности. Пусть 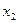 – вложения в рисковый актив. Тогда задача максимизации ожидаемой полезности индивида имеет вид:
– вложения в рисковый актив. Тогда задача максимизации ожидаемой полезности индивида имеет вид:
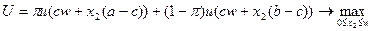 .
.
Условия первого порядка, характеризующие оптимальную величину вложений в рисковый актив 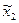 , имеют вид:
, имеют вид:
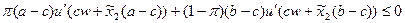 при
при 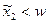
и
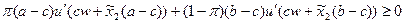 при
при 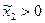
1) Для индивида-рискофоба условие 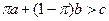 является необходимым и достаточным условием положительного спроса на рисковый актив.
является необходимым и достаточным условием положительного спроса на рисковый актив.
2) Индивид нейтральный к риску при 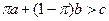 вкладывает все средства в рисковый актив, а при
вкладывает все средства в рисковый актив, а при 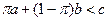 вкладывает все средства в безрисковый актив.
вкладывает все средства в безрисковый актив.
Модель с контингентными благами. Назовем контингентным благ ом 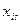 право (контракт) на получение
право (контракт) на получение 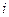 -го физического блага в количестве
-го физического блага в количестве 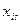 в случае реализации состояния природы
в случае реализации состояния природы 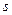 . В случае одного физического блага (денег) деньги (богатство) в разных состояниях мира – это разные контингентные блага.
. В случае одного физического блага (денег) деньги (богатство) в разных состояниях мира – это разные контингентные блага.
Тогда задача потребителя сводится как выбору наилучшего из доступных наборов контингентных благ, причем набор контингентных благ 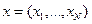 , где
, где 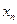 - это богатство индивида в состоянии мира
- это богатство индивида в состоянии мира 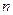 ,
, 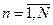 , не хуже набора
, не хуже набора 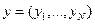 , когда ожидаемая полезность от набора
, когда ожидаемая полезность от набора 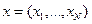 не меньше ожидаемой полезности от набора
не меньше ожидаемой полезности от набора 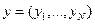 , т.е.
, т.е. 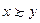
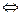
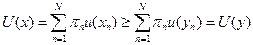 . Множество доступных наборов контингентных благ описывается бюджетным множеством.
. Множество доступных наборов контингентных благ описывается бюджетным множеством.
В случае модели формирования портфеля инвестиций (из рискового и безрискового активов) есть два контингентных блага: 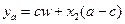 и
и 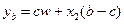 . Уравнение бюджетной линии в пространстве контингентных благ имеет вид:
. Уравнение бюджетной линии в пространстве контингентных благ имеет вид: 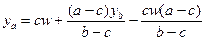 при
при 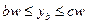 .
.
 2014-02-02
2014-02-02 531
531







