План
Темы: Выбор потребителя в условиях неопределенности
- Описание модели спроса на рисковый актив в терминах контингентных благ.
- Модель спроса на страховку.
1. Назовем контингентным благ ом богатство индивида в случае реализации состояния мира 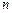 . Тогда потребитель выбирает между наборами контингентных благ
. Тогда потребитель выбирает между наборами контингентных благ 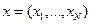 , где
, где 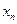 - это богатство индивида в состоянии мира
- это богатство индивида в состоянии мира 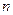 ,
, 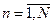 . Предпочтения на наборах контингентных благ описываются (обобщенной) функцией ожидаемой полезности: набор контингентных благ
. Предпочтения на наборах контингентных благ описываются (обобщенной) функцией ожидаемой полезности: набор контингентных благ 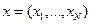 не хуже набора
не хуже набора 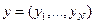 , когда ожидаемая полезность от набора
, когда ожидаемая полезность от набора 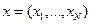 не меньше ожидаемой полезности от набора
не меньше ожидаемой полезности от набора 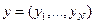 , т.е.
, т.е. 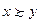

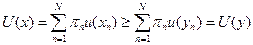 . Множество доступных наборов контингентных благ описывается бюджетным ограничением.
. Множество доступных наборов контингентных благ описывается бюджетным ограничением.
В случае модели формирования портфеля инвестиций (из рискового и безрискового активов, см. описание в плане лекции 12) есть два состояния мира и, соответственно, два контингентных блага: 1) 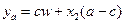 - богатство в состоянии мира, когда рисковый актив имеет доходность
- богатство в состоянии мира, когда рисковый актив имеет доходность 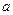 , и 2)
, и 2) 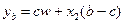 - богатство в состоянии мира, когда рисковый актив имеет доходность
- богатство в состоянии мира, когда рисковый актив имеет доходность 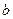 . Уравнение бюджетной линии в пространстве контингентных благ имеет вид:
. Уравнение бюджетной линии в пространстве контингентных благ имеет вид: 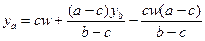 при
при 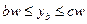 . Заметим, что индивиду всегда должен быть доступен набор контингентных благ, соответствующий ситуации, когда он не рискует, т.е. все средства вкладывает в безрисковый актив (точка первоначального запаса). В этом случае не зависимо от того, какое состояние мира наступит доход индивида составит
. Заметим, что индивиду всегда должен быть доступен набор контингентных благ, соответствующий ситуации, когда он не рискует, т.е. все средства вкладывает в безрисковый актив (точка первоначального запаса). В этом случае не зависимо от того, какое состояние мира наступит доход индивида составит 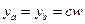 , т.е. набор контингентных благ
, т.е. набор контингентных благ 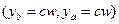 соответствует случаю
соответствует случаю 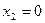 . Поскольку по условию вложения в рисковый актив должны удовлетворять ограничению
. Поскольку по условию вложения в рисковый актив должны удовлетворять ограничению 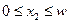 , то другой крайний случай,
, то другой крайний случай, 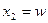 , соответствует набору контингентных благ
, соответствует набору контингентных благ 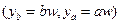 .
.
Кривая безразличия по определению – это множество наборов контингентных благ, дающих один и тот же уровень ожидаемой полезности, т.е. это все такие наборы 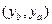 , что
, что 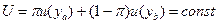 . Соответственно, наклон кривой безразличия (с обратным знаком) описывается предельной нормой замещения
. Соответственно, наклон кривой безразличия (с обратным знаком) описывается предельной нормой замещения 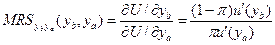 , причем в любой точке на линии определенности, где
, причем в любой точке на линии определенности, где 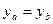 ,
, 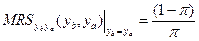 . Если индивид является рискофобом, то элементарная функция полезности (а, следовательно, и функция ожидаемой полезности) строго вогнута, а значит предпочтения выпуклы и множество наборов не хуже данного является выпуклым.
. Если индивид является рискофобом, то элементарная функция полезности (а, следовательно, и функция ожидаемой полезности) строго вогнута, а значит предпочтения выпуклы и множество наборов не хуже данного является выпуклым.
Тогда задачу индивида можно представить в виде задачи выбора наилучшего из доступных набора контингентных благ:
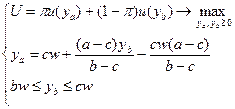 .
.
Внутренний оптимальный набор контингентных благ характеризуется касанием кривой безразличия и бюджетной линии, т.е. 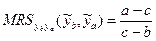 .
.
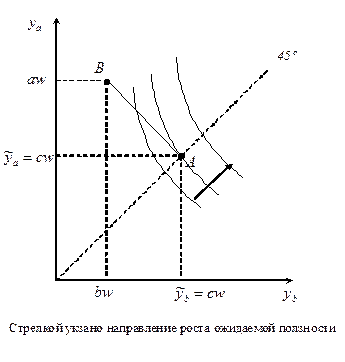
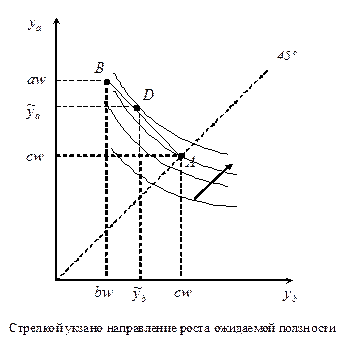
На левом рисунке изображен оптимальный выбор рискофоба при 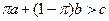 , на правом – при
, на правом – при 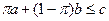 .
.
2. Модель спроса на страховку.
Рассмотрим индивида-рискофоба, предпочтения которого описываются ожидаемой функцией полезности с элементарной функцией полезности 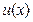 , где
, где 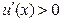 ,
, 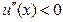 . Пусть богатство данного агента равно
. Пусть богатство данного агента равно 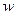 , однако существует возможность потери части этого богатства
, однако существует возможность потери части этого богатства 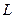 ,
, 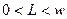 . Вероятность потери равна
. Вероятность потери равна 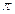 , где
, где 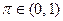 . Нейтральная к риску, не имеющая операционных издержек, страховая компания предлагает страховку по цене
. Нейтральная к риску, не имеющая операционных издержек, страховая компания предлагает страховку по цене 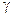 за каждую единицу страхового покрытия. Пусть
за каждую единицу страхового покрытия. Пусть 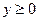 - это количество страховки, покупаемой индивидом, т.е. величина страхового покрытия (иногда вводится дополнительное предположение, что страховое покрытие не может быть больше потерь, т.е.
- это количество страховки, покупаемой индивидом, т.е. величина страхового покрытия (иногда вводится дополнительное предположение, что страховое покрытие не может быть больше потерь, т.е. 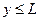 ):
):
Задача индивида: 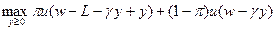
В оптимальной точке 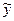 выполнены условия первого порядка (необходимые и достаточные, поскольку целевая функция строго вогнута):
выполнены условия первого порядка (необходимые и достаточные, поскольку целевая функция строго вогнута):
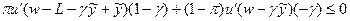
и 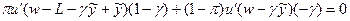 , если
, если 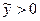 .
.
Утверждение: Если страховка актуарно справедлива, т.е. 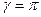 (в этом случае ожидаемая прибыль страховой компании равна нулю), то индивид-рискофоб страхуется полностью, т.е.
(в этом случае ожидаемая прибыль страховой компании равна нулю), то индивид-рискофоб страхуется полностью, т.е. 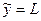 .
.
Утверждение: Если страховка не является актуарно справедливой, т.е. 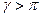 (в этом случае ожидаемая прибыль страховой компании положительна), то индивид-рискофоб (с дифференцируемой элементарной функцией полезности) застрахуется на сумму, меньшую потерь, т.е.
(в этом случае ожидаемая прибыль страховой компании положительна), то индивид-рискофоб (с дифференцируемой элементарной функцией полезности) застрахуется на сумму, меньшую потерь, т.е. 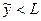 .
.
 2014-02-02
2014-02-02 3651
3651







