П.9. Нахождение кратчайших путей. Алгоритм Дейкстры

Лекция 9.

До сих пор мы рассматривали графы, в которых нас интересовали вершины и ребра (дуги), по которым можно перемещаться. Теперь можно рассматривать не только перемещение из одной вершины в другую, но и то, как это сделать наилучшим способом. Первый вопрос состоит, конечно, в том, что означает «наилучшим способом». Это может быть самый дешевый путь, самый безопасный путь, кратчайший путь или тот, который требует минимум энергии, или путь, выбранный в соответствии с каким-то иным критерием.

Для решения такого класса задач рассматриваются взвешенные графы (орграфы), ребрам (дугам) которых приписан некоторый вес. Общий подход к решению задачи о кратчайшем пути был развит американским математиком Ричардом Беллманом (1920 – 1984), который предложил для этого вида задач название динамическое программ-мирование. Задача о кратчайшем пути – это частный случай задачи, которую можно сформулировать следующим образом. Формулировка задачи: найти в заданном графе пути, соединяющие две заданные вершины и доставляющие минимум или максимум некоторой аддитивной функции, определенной на путях. Чаще всего эта функция трактуется как длина пути, и задача называется задачей о кратчайших путях.

Алгоритм Дейкстры (Едсгер Дейкстра, нидерландский математик, 1930 – 2002) является одной из реализаций этой задачи. Его часто еще называют алгоритмом расстановок меток.

Пусть 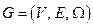– ориентированный граф с взвешенными дугами. Обозначим s -вершину – начало пути и t -вершину – конец пути. В процессе работы алгоритма Дейкстры вершинам орграфа x_i Î V приписываются числа (метки) d (x_i), которые служат оценкой длины (веса) кратчайшего пути от вершины s к вершине x_i. Если вершина x_i получила на некотором шаге метку d (x_i), это означает, что в графе G существует путь из s в x_i, имеющий вес d (x_i). Метки могут находиться в двух состояниях – быть временными или постоянными. Превращение метки в постоянную означает, что кратчайшее расстояние от вершины s до соответствующей вершины найдено. Алгоритм Дейкстры содержит одно ограничение – веса дуг должны быть положительными. Сам алгоритм состоит из двух этапов. На первом находится длина кратчайшего пути, на втором строится сам путь от вершины s к вершине t.