а) По данной матрице весов изображаем орграф G, который не будет являться взвешенным

б) Находим полустепень исхода и полустепень захода для каждой вершины.
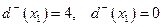 ;
; 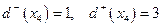 ;
; 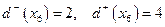 ;
;
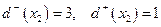 ;
; 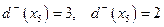 ;
; 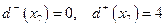 .
.
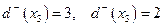 ;
;
Так как вершина x 1 имеет 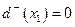 , то эта вершина является истоком. Так как вершина x 7 имеет
, то эта вершина является истоком. Так как вершина x 7 имеет 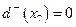 , то эта вершина является стоком.
, то эта вершина является стоком.
в) Построим матрицу смежности вершин. Данный орграф имеет семь вершин, поэтому матрица смежности вершин 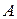 является квадратной матрицей седьмого порядка. Для заполнения первой строки матрицы
является квадратной матрицей седьмого порядка. Для заполнения первой строки матрицы 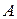 найдем число дуг, соединяющих первую вершину с каждой из остальных вершин.
найдем число дуг, соединяющих первую вершину с каждой из остальных вершин.
Поскольку количество дуг, исходящих из первой вершины в первую равно 0 (в орграфе нет петель, соответствующих первой вершине), исходящих из первой во вторую равно 1, из первой в третью равно 0, из первой в четвертую равно 1, из первой в пятую равно 1, из первой в шестую равно 1, из первой в седьмую равно 0, то первая строка матрицы 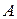 имеет вид (0 1 0 1 1 1 0). Заполняя аналогично остальные строки, получаем матрицу
имеет вид (0 1 0 1 1 1 0). Заполняя аналогично остальные строки, получаем матрицу  вида:
вида:
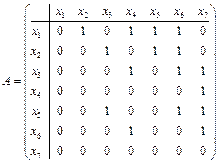 .
.
Так как орграф имеет шестнадцать дуг, то матрица смежности дуг 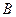 является квадратной матрицей шестнадцатого порядка. Дуга u 1 предшествует дугам u 5, u 6 и u 7. Поэтому первая строка матрицы
является квадратной матрицей шестнадцатого порядка. Дуга u 1 предшествует дугам u 5, u 6 и u 7. Поэтому первая строка матрицы 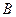 имеет вид (0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0). Заполняем аналогично остальные строки, получаем матрицу
имеет вид (0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0). Заполняем аналогично остальные строки, получаем матрицу  вида:
вида:
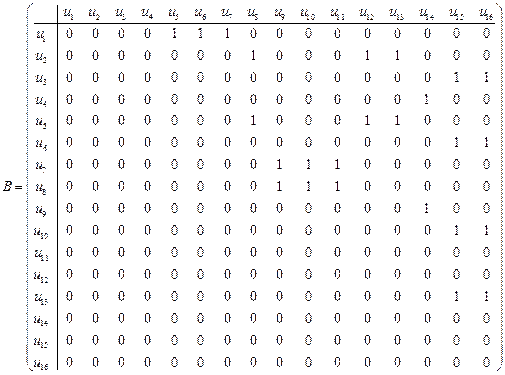 .
.
Орграф имеет семь вершин и шестнадцать дуг, поэтому матрица инциденций 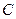 является матрицей размерности 7´16. Поскольку вершина
является матрицей размерности 7´16. Поскольку вершина 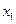 инцидентна дугам
инцидентна дугам 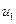 ,
, 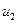 ,
, 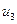 и
и 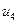 , которые выходят из вершины
, которые выходят из вершины 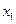 , и не инцидентна остальным дугам, то первая строка матрицы
, и не инцидентна остальным дугам, то первая строка матрицы 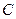 имеет вид (1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0). Остальные строки матрицы заполняем аналогично, учитывая то, в каких случаях вершина
имеет вид (1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0). Остальные строки матрицы заполняем аналогично, учитывая то, в каких случаях вершина 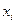 будет началом, а в каких случаях концом дуги
будет началом, а в каких случаях концом дуги 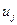 . Следовательно, матрица
. Следовательно, матрица 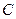 имеет вид:
имеет вид:
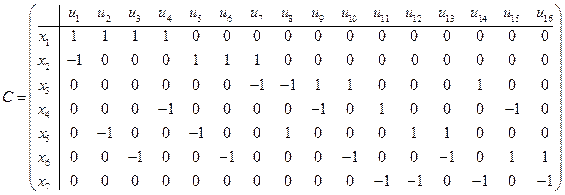 .
.
г) Чтобы найти величину минимального пути и сам путь от вершины s = x 1 до вершины t=x 7 с помощью алгоритма Дейкстры, построим орграф, у которого к каждой дуге припишем ее вес.
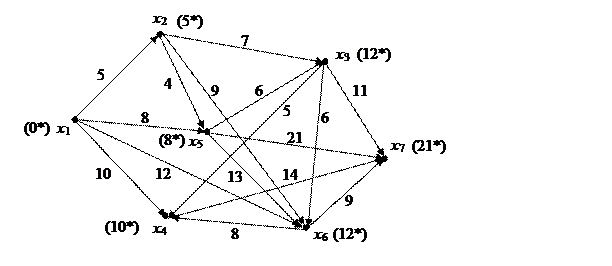
 2014-02-02
2014-02-02 625
625








