Шаг 5. Последовательный поиск дуг кратчайшего пути.
Среди вершин, непосредственно предшествующих вершине 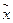 с постоянными метками, находим вершину xi, удовлетворяющую соотношению
с постоянными метками, находим вершину xi, удовлетворяющую соотношению
 .
.
Включаем дугу  в искомый путь и полагаем
в искомый путь и полагаем 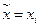 .
.
Если 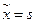 , то кратчайший путь найден – его образует последовательность дуг, полученных на пятом шаге и выстроенных в обратном порядке. В противном случае возвращаемся к пятому шагу.
, то кратчайший путь найден – его образует последовательность дуг, полученных на пятом шаге и выстроенных в обратном порядке. В противном случае возвращаемся к пятому шагу.
Пример 9.1. По заданной матрице весов 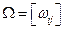 :
:
а) построить ориентированный граф;
б) найти полустепень захода и полустепень исхода каждой вершины;
в) построить матрицу смежности вершин, матрицу смежности дуг, матрицу инциденций;
г) найти величину минимального пути и сам путь от вершины s = x 1 до вершины t=x 7 с помощью алгоритма Дейкстры.
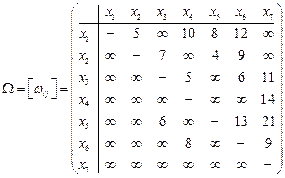 .
.
 2014-02-02
2014-02-02 323
323








