План
Примерный план лекции №4 и основные определения.
Темы: Теория поведения потребителя: случай натурального дохода; экономика обмена (начало)
- Бюджетное ограничение и задача потребителя в случае натурального дохода.
- Экономика обмена: допустимые распределения, ящик Эджворта, Парето-оптимальные распределения.
1. Поведение потребителя в случае натурального дохода. Предположим, что индивид обладает некоторым запасом благ 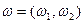 , которые предлагаются на рынке по ценам
, которые предлагаются на рынке по ценам 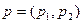 , и не имеет фиксированного дохода, тогда бюджетное ограничение потребителя имеет вид:
, и не имеет фиксированного дохода, тогда бюджетное ограничение потребителя имеет вид: 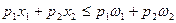 . Графически, бюджетная линия проходит через точку первоначального запаса точка
. Графически, бюджетная линия проходит через точку первоначального запаса точка 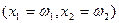 и имеет наклон
и имеет наклон 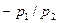 . Решение задачи потребителя, набор
. Решение задачи потребителя, набор 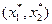 , теперь зависит как от цен, так и от первоначального запаса благ:
, теперь зависит как от цен, так и от первоначального запаса благ: 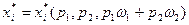 .
.
Если 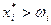 , то говорят, что потребитель является чистым покупателем или чистым потребителем данного блага.
, то говорят, что потребитель является чистым покупателем или чистым потребителем данного блага.
Если 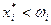 , то говорят, что потребитель является чистым продавцом или чистым поставщиком данного блага.
, то говорят, что потребитель является чистым продавцом или чистым поставщиком данного блага.
В экономике с двумя благами при положительных ценах потребитель не может быть чистым покупателем или чистым продавцом обоих благ одновременно.
2. Экономика обмена. Обозначим через 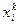 потребление блага
потребление блага 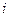 ,
,  потребителем
потребителем 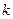 ,
, 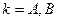 , а через
, а через 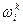 - первоначальный запас блага
- первоначальный запас блага 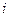 у потребителя
у потребителя 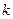 .
.
Распределением называется пара потребительских наборов 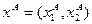 и
и 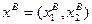 , т.е.
, т.е. 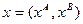 .
.
Распределение называется допустимым, если потребляемое количество каждого блага равно совокупному запасу этого блага, т.е. 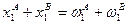 и
и 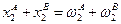 .
.
Допустимое распределение  называется Парето-оптимальным (эффективным), если нельзя улучшить положение одного потребителя, не ухудшая положение другого. Другими словами, распределение
называется Парето-оптимальным (эффективным), если нельзя улучшить положение одного потребителя, не ухудшая положение другого. Другими словами, распределение  Парето-оптимально, если для него нельзя построить Парето-улучшение, т.е. не существует другого допустимого распределения
Парето-оптимально, если для него нельзя построить Парето-улучшение, т.е. не существует другого допустимого распределения 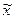 такого, что
такого, что 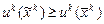 для всех потребителей и хотя бы для одного потребителя
для всех потребителей и хотя бы для одного потребителя 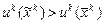 .
.
Дифференциальная характеристика Парето-оптимальных распределений:
1) Если функции полезности потребителей дифференцируемы, то во внутреннем Парето-оптимальном распределении 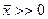 (т.е. таком, где объем потребления каждого блага каждым потребителем положителен) выполнено:
(т.е. таком, где объем потребления каждого блага каждым потребителем положителен) выполнено: 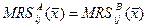 . Т.е. в случае экономики обмена с двумя потребителями и двумя благами во внутреннем Парето-оптимуме имеет место касание кривых безразличия.
. Т.е. в случае экономики обмена с двумя потребителями и двумя благами во внутреннем Парето-оптимуме имеет место касание кривых безразличия.
Условие равенства предельных норм замещение – необходимое и достаточное условие внутреннего Парето-оптимума, если предпочтения потребителей выпуклы (т.е. для любого набора 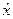 из множества допустимых наборов
из множества допустимых наборов 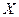 множество наборов не хуже
множество наборов не хуже 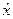 выпукло).
выпукло).
Пример ситуации, когда предпочтения одного потребителя (А) не являются выпуклыми и из равенства предельных норм замещения получаем не Парето-оптимальное распределение:
Итак, пусть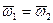 ,
, 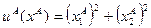 и
и 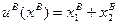 . Тогда
. Тогда 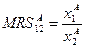 ,
, 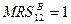 . И из равенства предельных норм замещения получаем:
. И из равенства предельных норм замещения получаем: 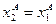 , т.е. диагональ ящика Эджворта. Однако распределения на диагонали Парето-улучшаемы. В действительности, в данном случае нет внутренних Парето-оптимальных распределений; множество Парето-оптимальных распределений – периметр (все стенки) ящика Эджворта.
, т.е. диагональ ящика Эджворта. Однако распределения на диагонали Парето-улучшаемы. В действительности, в данном случае нет внутренних Парето-оптимальных распределений; множество Парето-оптимальных распределений – периметр (все стенки) ящика Эджворта.
2) Граничные Парето-оптимальные распределения: Пусть 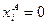 ,
, 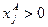 ,
, 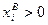 ,
,  , где
, где 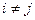 , тогда
, тогда 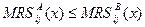 . Если
. Если 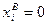 ,
,  ,
, 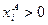 ,
, 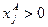 , где
, где 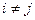 , то получаем следующую характеристику граничного Парето-оптимума
, то получаем следующую характеристику граничного Парето-оптимума 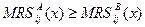 .
.
Пример. Пусть 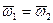 ,
, 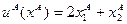 и
и 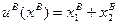 . Тогда в любой точке ящика Эджворта
. Тогда в любой точке ящика Эджворта 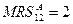 и
и 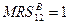 . Внутренних Парето-оптимальных распределений нет. Граничные Парето-оптимальные распределения – все наборы такие, что
. Внутренних Парето-оптимальных распределений нет. Граничные Парето-оптимальные распределения – все наборы такие, что 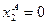 при
при 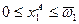 , и
, и 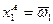 при
при 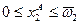 (т.е. нижняя и правая стенки ящика Эджворта).
(т.е. нижняя и правая стенки ящика Эджворта).
Пример: Поиск Парето-оптимальных распределений в экономике обмена, где предпочтения потребителей описываются функциями полезности Кобба-Дугласа:
Пусть 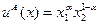 и
и 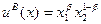 , где
, где 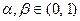 ,
,  .
.
1) Граничные Парето-оптимальные распределения: только две точки начала координат для потребителей А и В, т.е. точки 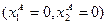 и
и 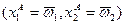 .
.
2) Внутренние Парето-оптимальные распределения: поскольку предпочтения выпуклые, то во внутреннем Парето-оптимуме 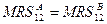 . Таким образом, для поиска внутренних Парето-оптимальных распределений нужно решить систему:
. Таким образом, для поиска внутренних Парето-оптимальных распределений нужно решить систему:
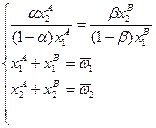 ,
,
откуда находим: 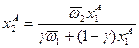 , где
, где 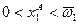 и
и 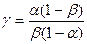 .
.
Тогда множество Парето-оптимальных распределений (внутренних и граничных) описывается функцией 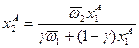 при
при 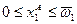 . При
. При 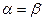 множество Парето-оптимальных распределений совпадает с диагональю ящика Эджворта,
множество Парето-оптимальных распределений совпадает с диагональю ящика Эджворта, 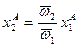 . При
. При 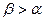 , кривая лежит выше диагонали (функция строго вогнута), при
, кривая лежит выше диагонали (функция строго вогнута), при 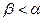 кривая лежит ниже диагонали (функция строго выпукла).
кривая лежит ниже диагонали (функция строго выпукла).
Утверждение (задача на поиск Парето-оптимальных распределений в экономике с 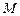 потребителями и
потребителями и 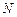 благами)[1]. Пусть предпочтения каждого потребителя представимы функцией полезности, которая является дважды непрерывно дифференцируемой, причем предпочтения потребителей строго монотонны. Обозначим через
благами)[1]. Пусть предпочтения каждого потребителя представимы функцией полезности, которая является дважды непрерывно дифференцируемой, причем предпочтения потребителей строго монотонны. Обозначим через 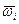 совокупный запас блага
совокупный запас блага 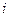 . Будем также считать, что
. Будем также считать, что 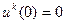 . Рассмотрим следующую задачу:
. Рассмотрим следующую задачу:
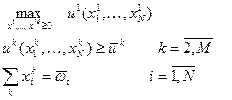 (1)
(1)
Каждое решение задачи (1) является Парето-оптимальным распределением и наоборот, любое Парето-оптимальное распределение является решением задачи (1) при некоторых значениях уровней полезности 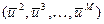 .
.
[1] Знание этого утверждения не является обязательным.
 2014-02-02
2014-02-02 707
707







