Двойственность. Класс самодвойственных функций.
Лекция 2
Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.
Будем называть операцию конъюнкции двойственной операции дизъюнкции, а операцию дизъюнкции
двойственной операции конъюнкции. Определение. Формулы А и А * называются двойственными, если формула А * получается из формулы А путем замены в ней каждой операции на двойственную.
Например, для формулы А º (х Úy)&z двойственной формулой будет формула А * º (х& у) Ú z.
Теорема. Если формулы А и В равносильны, то равносильны и им двойственные формулы, то есть
А* º В *.
Предварительно докажем лемму.
Лемма. Если для формулы A(x1,x2....xn) двойственной формулой является А*(x1,x2....xn), то справедлива равносильность А*(x 1,..., xn) = 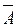 (
(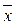 1,...,
1,..., 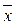 n).
n).
(Доказательство леммы разбирается студентом самостоятельно см. Лихтарников «МЛ» стр. 28-29)
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
| x | f | f * |
Функции f (x) = x и g (x) = 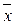 двойственны сами себе:
двойственны сами себе:
| x | f | f * | g | g * |
так как f *(0)=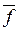 (1).
(1).
Определение 1. Если f *(x 1,..., xn) = f (x 1,..., xn), то f (x 1,..., xn) называется самодвойственной.
Множество всех самодвойственных функций обозначается через S.
Если f *– самодвойственна, то  (
(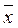 1,...,
1,..., 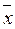 n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
Пример 1. Покажем, что функция х 1Ú х 2 двойственна к x 1& x 2, функция х 1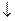 х 2 двойственна к функции x 1| x 2.
х 2 двойственна к функции x 1| x 2.
| x 1 | x 2 | f = х 1Ú х 2 | f * | g = x 1| x 2 | g *= x 1 x 2 x 2 |
Пример 2. Построить формулу, реализующую f *, если f = ((x 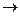 y) Ú z) (y
y) Ú z) (y 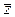
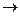 (xÅyz)). Покажем, что она эквивалентна формуле N = z (x Å y).
(xÅyz)). Покажем, что она эквивалентна формуле N = z (x Å y).
Найдем (x Å y)* и (x 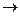 y)*.
y)*.
| x | y | xÅy | (x Å y)* | x 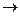 y y | (x 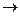 y)* y)* |
Из таблиц видно, что
(x 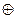 y)* = x ~ y =
y)* = x ~ y = 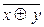 = x
= x 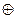 y
y 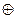 1, x
1, x 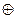 y =
y =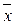 y
y 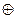 x
x 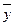 ,
,
(x 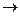 y)* =
y)* =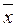 y x
y x 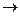 y =
y =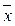
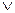 y.
y.
По принципу двойственности:
f * = 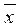 yz
yz 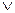 (
(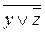 (x
(x 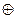 (y
(y 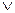 z)
z)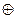 1)) =
1)) = 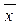 yz
yz 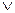
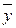 z (x
z (x 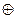 (y
(y 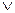 z)
z)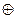 1) = z (
1) = z (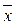 y Ú(
y Ú(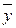 x Å
x Å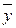 z Å
z Å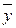 )) = z (
)) = z (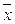 y Ú
y Ú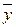 (x Å z Å1)) = z (
(x Å z Å1)) = z (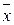 y Ú
y Ú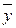 (x Å
(x Å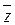 )) = z
)) = z 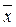 y Ú(z
y Ú(z 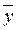 x Å z
x Å z 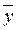
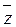 ) = z (
) = z (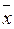 y Ú x
y Ú x 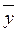 ) = z (x Å y).
) = z (x Å y).
Тогда f = (f *)* = [ z (x Å y)]* = z Ú(x ~ y).
Обозначим множество всех функций двузначной алгебры логики Р2. Обозначим через Р2(n) число функций, зависящих от n переменных. Очевидно, Р2(n)=22 n.
Определение. Система функций { f 1, f 2,..., f s,...}Ì P 2 называется полной в Р 2, если любая функция f (x 1,..., xn) Î P 2 может быть записана в виде формулы через функции этой системы.
Примеры полных систем:
1. P 2 – полная система.
2. Система M ={ x 1& x 2, x 1Ú x 2, 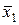 } – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.
} – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.
Примерами неполных систем являются: { 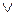 }, {0,1}.
}, {0,1}.
Лемма (достаточное условие полноты)
Пусть система  U = { f 1, f 2,..., fs,...} полна в Р 2. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
U = { f 1, f 2,..., fs,...} полна в Р 2. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
Данная лемма может быть использована следующим образом:
1. Покажем, что система { x 1Ú x 2, 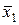 } – полна в P 2.
} – полна в P 2.
Возьмем в качестве полной в Р 2 системы U ={ x 1Ú x 2, 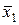 , x 1& x 2}, B ={ x 1Ú x 2,
, x 1& x 2}, B ={ x 1Ú x 2, 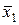 }. Надо показать, что x 1& x 2 представляется формулой над B. Действительно, по правилу Де Моргана получим: x 1& x 2=
}. Надо показать, что x 1& x 2 представляется формулой над B. Действительно, по правилу Де Моргана получим: x 1& x 2=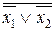 .
.
2. Система { x 1| x 2} полна в Р 2. Для доказательства возьмем в качестве полной в Р 2 системы U = { x 1& x 2, 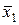 } и выразим х 1& х 2 и
} и выразим х 1& х 2 и 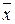 через х 1| x 2 :
через х 1| x 2 : 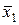 = x 1 | x 1, x 1 & x 2 =
= x 1 | x 1, x 1 & x 2 =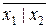 = (x 1| x 2)|(x 1| x 2).
= (x 1| x 2)|(x 1| x 2).
3. Система { x 1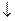 x 2} полна в Р 2. U = { x 1Ú x 2,
x 2} полна в Р 2. U = { x 1Ú x 2, 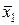 },
}, 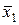 = x 1
= x 1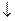 x 1, x 1Ú x 2 =
x 1, x 1Ú x 2 = 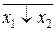 = (x 1
= (x 1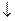 x 2)
x 2) 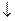 (x 1
(x 1 x 2).
x 2).
7. Система { x 1& x 2, x 1Å x 2, 0, 1}, U = { x 1& x 2, 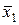 },
}, 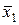 = x 1Å1.
= x 1Å1.
Следствие. Полином Жегалкина.
f (x 1,..., xn) Ì P 2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как { x 1& x 2, x 1Å x 2, 0, 1} полна в Р 2. В силу свойства x & (yÚz) = xy Ú xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х 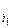 х
х 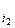 ... х
... х 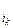 , соединенных знаком Å. Такой полином называется полиномом Жегалкина.
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
Общий вид полинома Жегалкина: 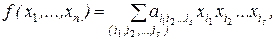 где
где 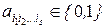 , s = 0, 1,..., n, причем при s = 0 получаем свободный член а 0.
, s = 0, 1,..., n, причем при s = 0 получаем свободный член а 0.
 2014-02-02
2014-02-02 2557
2557