2014-02-02
368
Вероятности сложных событий
Лекция № 3
Часто возникает ситуация, когда вероятность искомого события может быть вычислена через известные вероятности ряда более простых событий, наступление или отсутствие которых приводит к искомому событию.
Начнем с определения.
Определение. Если 
>
, то частное 
называется условной вероятностью события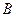 
при условии 
(или условной вероятностью события 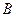при условии, что событие произошло).
Оно обозначается:
.
Смысл условной вероятности открывается из следующего рассуждения. Пусть рассматриваются геометрические вероятности. Событие состоит в том, что бросаем точку на часть плоскости 
и попадаем в фигуру , а событие 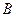- попадаем в фигуру 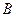(см. рис. 3.1). Событие 
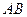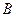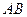состоит в том, что бросаем точку и она попадает в общую часть фигур и (на рис. 3.1 эта часть забита точками). Тогда характеризует, какую часть по отношению к части (событию ) составляет часть (событие ).
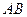Рис 3.1. Иллюстрация понятия условной вероятности
Иными словами,
.
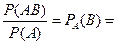
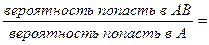
Вывод из сказанного получается следующий: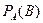 
действительно обозначает вероятность того, что 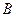произойдёт при условии, что произошло.
