Теорема сложения вероятностей событий

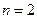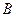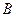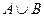Начнем с геометрической иллюстрации. Пусть рассматривается геометрическая вероятность в случае (плоский случай). Событие состоит в том, что бросаем точку на часть плоскости и попадаем в фигуру , а событие - попадаем в фигуру (см. рис. 3.2). Найдем вероятность того, что бросаем точку в область и попадаем в фигуру , т.е. забитую точками на рис. 3.2 фигуру. Эта фигура 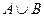соответствует событию, состоящему в наступлении или события или события 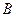, т.е. события .

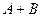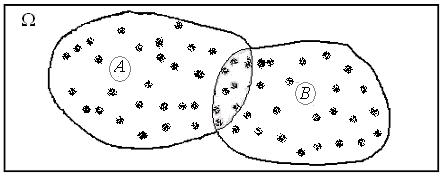
Рис. 3.2. Иллюстрация к теореме сложения вероятностей

В силу геометрической вероятности эта вероятность 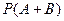равна:

,

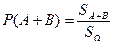где 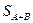- площадь фигуры 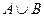, а 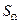- площадь области . Осталось найти площадь 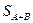. Она равна:

,

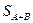
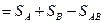где 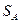- площадь фигуры , 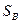- площадь фигуры 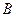, 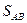- площадь общей части фигур и 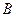, «забитой» на рис. 3.2 пятнами. Тогда:

,

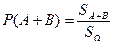
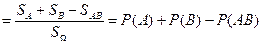где по определению геометрической вероятности:

вероятность события ,

вероятность события ,

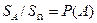
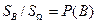
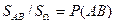
вероятность события .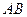

Тем самым, мы приходим к равенству

,

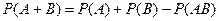которое и составляет содержание теоремы о сложении вероятностей совместных событий, но доказательство её в общем случае гораздо сложнее и его мы оставляем без внимания.

Теорема о сложении вероятностей совместных событий. Вероятность суммы совместных событий и 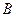равна:

.

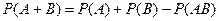Здесь слова «вероятность совместных событий» имеют принципиальное значение, т.к. для несовместных событий получается несколько иная теорема. Разберёмся в этом. Для несовместных событий и 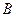основным свойством является равенство (они вместе произойти не могут):

.

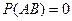Поэтому теорема переписывается в следующем виде.

Теорема о сложении вероятностей несовместных событий. Вероятность суммы несовместных событий и 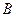равна:

.

___________________________________________

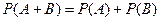Пример. «Не кладите все яйца в одну корзину». В два банка положены деньги (слава Богу, что некто догадался положить их именно в два банка). Банки работают независимо друг от друга (часто встречающаяся ситуация). Вероятность разорения первого банка равна 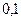, а второго - 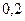. Какова вероятность того, что деньги сохранятся хотя бы в одном из банков.

Решение. Чтобы решить вероятностную задачу, главное, ввести правильные обозначения. Попробуем ввести следующие события.

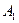- деньги взяты из первого банка,

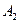- деньги взяты из второго банка.

Тогда событие 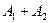означает, что деньги взяты либо из первого, либо из второго банка, либо из обоих банков сразу (вам очень повезло). А найти нужно именно вероятность этого события 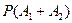. По формуле сложения вероятностей совместных событий получаем:

.

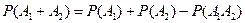Вероятность 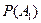того, что первый банк останется «на плаву», составляет с вероятностью 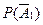того, что первый банк разорится, в сумме 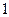(т.к. событие есть достоверное событие). Поэтому:

.

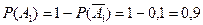Аналогично найдем

.

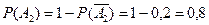А вероятность произведения двух событий 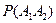равна произведению вероятностей 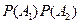, как произведение независимых событий. Поэтому:

.

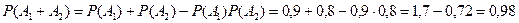То есть искомая вероятность получается больше вероятносте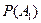й и 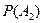, а, значит, права пословица!