2014-02-02
330
Предположим, что функция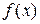 
непрерывна на отрезке 
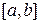. Будем рассматривать интегралы от этой функции на отрезках 
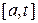при всевозможных 
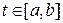. Очевидно, что результат интегрирования зависит от значения верхнего предела интегрирования. Поэтому обозначим 
. Имеем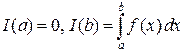 
.
Рассмотрим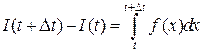 
. В соответствии с теоремой о среднем существует такое значение 
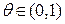, что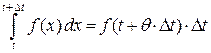 
. Следовательно, 
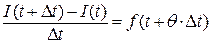. Переходя в последнем равенстве к пределу при 
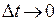и пользуясь непрерывностью функции 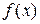в точке 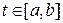, получим
.
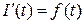Последнее означает, что функция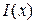 
является первообразной для функции 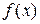. Следовательно, если 
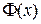– любая первообразная функции 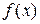, то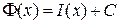 
по свойству двух первообразных одной и той же функции. Следовательно, 
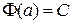, так как 
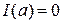, и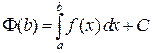 
. Значит,
.
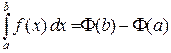Последняя формула, называемая формулой Ньютона-Лейбница, как раз обеспечивает связь между интегралом Римана (его еще называют определенным интегралом) и первообразными. Формулу Ньютона-Лейбница еще записывают в виде
,
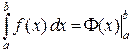где вертикальная черта и индексы обозначают разность значений функций, соответственно, при верхнем и нижнем значениях переменной.
