Приложения интеграла Римана
Интеграл Римана по отрезку был нами введен как площадь криволинейной трапеции. Понятие площади неотделимо от понятия интеграла. С его помощью можно вычислять площади любых плоских областей, а также длины дуг, площади поверхностей и объемы тел.
1.Вычислить площадь области, расположенной между двумя кривыми 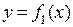 и
и 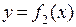 и над отрезком
и над отрезком 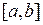 , причем
, причем 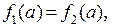
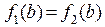 .
.

Очевидно, что площадь области между кривыми равна разности площадей соответствующих криволинейных трапеций, поэтому
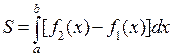 .
.
2. Вычислить площадь криволинейного сектора, ограниченного лучами (в полярных координатах) 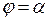 и
и 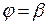 , а также заданной в полярных координатах кривой
, а также заданной в полярных координатах кривой 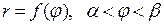 .
.
Проведем внутри криволинейного сектора лучи 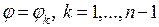 , разбивающие исходный сектор на мелкие криволинейные секторы
, разбивающие исходный сектор на мелкие криволинейные секторы 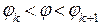 , причем
, причем 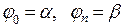 .
.
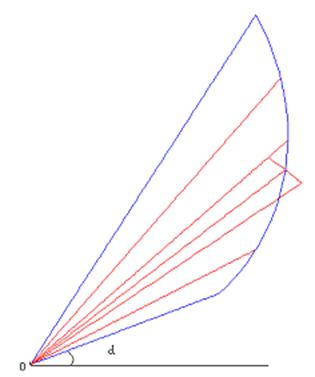
Заменим каждый мелкий криволинейный сектор круговым сектором с тем же углом при вершине и радиусом, равным значению 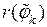 , где
, где 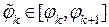 . Тогда площадь кругового мелкого сектора равна
. Тогда площадь кругового мелкого сектора равна 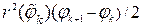 . При этом чем меньше разность
. При этом чем меньше разность 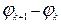 , тем меньше площадь кругового мелкого сектора отличается от площади соответствующего криволинейного мелкого сектора.
, тем меньше площадь кругового мелкого сектора отличается от площади соответствующего криволинейного мелкого сектора.
При достаточно частом разбиении исходного криволинейного сектора площадь его достаточно близка к величине
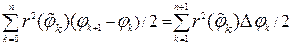 .
.
Если теперь устремить к нулю наименьший из растворов малых криволинейных секторов, мы получим предел интегральных сумм – интеграл 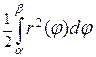 , который совпадает с площадью исходного криволинейного сектора.
, который совпадает с площадью исходного криволинейного сектора.
3.Вычислить длину дуги кривой 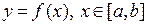 . Длиной дуги кривой мы будем называть предельную сумму длин вписанных в дугу хорд при стремлении этих хорд к точкам.
. Длиной дуги кривой мы будем называть предельную сумму длин вписанных в дугу хорд при стремлении этих хорд к точкам.
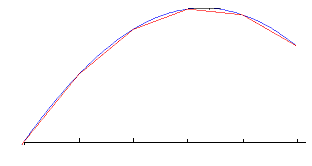
Разобъем отрезок 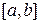 на
на 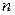 отрезков
отрезков 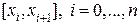 , где
, где 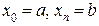 . Длина хорды, расположенной над отрезком
. Длина хорды, расположенной над отрезком 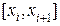 , равна
, равна 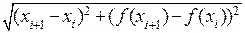 . Воспользуемся формулой конечных приращений Лагранжа и получим длину этой же хорды в виде
. Воспользуемся формулой конечных приращений Лагранжа и получим длину этой же хорды в виде
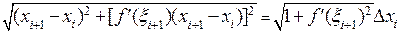 , где
, где 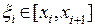 ,
,
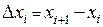 . Таким образом, длина дуги всей кривой может быть приближена суммой
. Таким образом, длина дуги всей кривой может быть приближена суммой 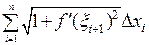 , причем чем мельче разбиение отрезка
, причем чем мельче разбиение отрезка 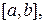 тем точнее результат. При стремлении длины наименьшего из отрезков разбиения к нулю мы получим из суммы интеграл:
тем точнее результат. При стремлении длины наименьшего из отрезков разбиения к нулю мы получим из суммы интеграл: 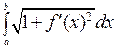 , который и дает выражение длины дуги данной кривой.
, который и дает выражение длины дуги данной кривой.
4. Вычислить длину дуги пространственной кривой, заданной параметрически в виде
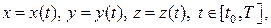
для вычисления ее длины применяют формулу
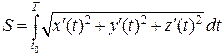 .
.
Пусть 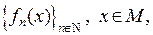 – последовательность функций, заданных на одном и том же множестве, причем при каждом значении
– последовательность функций, заданных на одном и том же множестве, причем при каждом значении  числовой ряд
числовой ряд 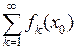 сходится. Тогда мы можем рассматривать функциональный ряд
сходится. Тогда мы можем рассматривать функциональный ряд 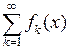 на множестве
на множестве  и исследовать свойства функции
и исследовать свойства функции 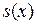 – суммы ряда – на том же множестве
– суммы ряда – на том же множестве  .
.
В связи с вопросами сходимости функциональных рядов отметим
следующий из теоремы сравнения мажорантный признак сходимости
функционального ряда: если 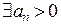 тчо
тчо 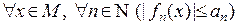 и ряд с положительными членами
и ряд с положительными членами 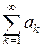 сходится, то функциональный ряд
сходится, то функциональный ряд 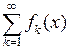 абсолютно сходится на множестве
абсолютно сходится на множестве  .
.
П р и м е р. Функциональный ряд 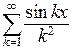 сходится при любом значении переменной
сходится при любом значении переменной  , так как мажорирующим рядом для него является сходящийся ряд
, так как мажорирующим рядом для него является сходящийся ряд 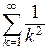 .
.
 2014-02-02
2014-02-02 445
445








