Пусть 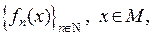 – последовательность функций, заданных на одном и том же множестве, причем при каждом значении
– последовательность функций, заданных на одном и том же множестве, причем при каждом значении 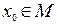 числовой ряд
числовой ряд 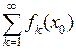 сходится. Тогда мы можем рассматривать функциональный ряд
сходится. Тогда мы можем рассматривать функциональный ряд 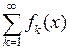 на множестве
на множестве 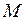 и исследовать свойства функции
и исследовать свойства функции 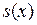 – суммы ряда – на том же множестве
– суммы ряда – на том же множестве 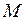 .
.
В связи с вопросами сходимости функциональных рядов отметим
следующий из теоремы сравнения мажорантный признак сходимости
функционального ряда: если 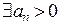 тчо
тчо 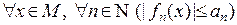 и ряд с положительными членами
и ряд с положительными членами 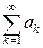 сходится, то функциональный ряд
сходится, то функциональный ряд 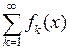 абсолютно сходится на множестве
абсолютно сходится на множестве 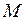 .
.
П р и м е р. Функциональный ряд 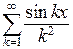 сходится при любом значении переменной
сходится при любом значении переменной 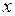 , так как мажорирующим рядом для него является сходящийся ряд
, так как мажорирующим рядом для него является сходящийся ряд 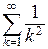 .
.
 2014-02-02
2014-02-02 306
306







