Волны – это процесс распространения колебаний. Природа колебаний определяет собой природу волнового процесса. Независимо от физической природы волновые процессы имеют одинаковое математическое описание. Механические волны представляют собой процесс распространения механических колебаний в упругих средах. Механические колебания частотного диапазона от 14 Гц до 20 кГц производят субъективные ощущения звука в органах слуха и по этой причине называются звуковыми или просто звуком. Соответствующие этому диапазону волны также называют звуковыми.
Основываясь на закономерностях гармонического анализа, сложный волновой процесс можно представить как суперпозицию простейших гармонических волн. По этой причине самые общие закономерности волновых процессов могут быть получены при изучении гармонических волн.
Гармонические волны есть результат распространения гармонических колебаний. Колебания, возбужденные в некоторой части упругой среды, благодаря наличию упругих связей между ее частицами, распространяются от источника колебаний на периферию со скоростью v передачи упругих взаимодействий в соответствующей среде. Так как вынужденные колебания совершаются с частотой вынуждающей силы, то постепенно все точки среды будут совершать те же колебания, что и центр, но с задержкой во времени 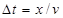 , где х – расстояние до соответствующей точки.
, где х – расстояние до соответствующей точки.
Распространение упругих волн в среде не связано с переносом вещества. В неограниченной среде оно состоит в вовлечении в вынужденные колебания все более и более удаленных от источника волн частей среды. При этом можно отвлечься от дискретного (молекулярного) строения среды, рассматривая ее как сплошную среду, непрерывно распределенную в пространстве и обладающую определенными упругими свойствами. Под частицей такой среды, совершающей вынужденные колебания, понимают малый элемент ее объема, размеры которого, однако, во много раз больше межмолекулярных расстояний, так что в нем содержится очень большое число молекул. Практически частицы среды можно считать точечными, так как даже в газе межмолекулярные расстояния крайне малы.
Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде - твердой, жидкой и газообразной. Примером являются звуковые волны в воздухе.
Упругая волна называется поперечной, если частицы среды колеблются перпендикулярно к направлению распространения волны. Поперечные волны связаны с деформацией сдвига и, следовательно, могут образовываться и распространяться только в твердых средах.
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении в ней рассматриваемой волны. Например, для волн в твердой среде такой величиной может служить вектор смещения частицы среды из положения равновесия или три его проекции на оси координат. Для характеристики продольных волн в газе или жидкости обычно пользуются избыточным давлением колеблющейся среды, равным разности между ее переменным и равновесным давлениями.
Лучом называется линия, касательная к которой в каждой ее точке совпадает с направлением распространения волны, т.е. с направлением переноса энергии волной. В однородной среде лучи имеют вид прямых линий.
Волновой поверхностью называется геометрическое место точек, в которых фаза колебаний имеет одно и то же значение. Для всех точек одной волновой поверхности величина Dt одинакова. Через каждую точку среды, охваченной волновым движением, можно провести одну волновую поверхность, соответствующую значению фазы колебаний в этой точке в рассматриваемый момент времени. Множеству различных значений фазы колебания соответствует семейство волновых поверхностей. В однородной изотропной среде волновые поверхности ортогональны лучам.
В волновом процессе колебания среды распространяются на все новые области. Поверхность, которой достигла волна в данный момент времени и которая разделяет собой точки возмущенной среды от точек среды, не охваченной волновым процессом, называется фронтом волны. Все точки фронта волны колеблются в одинаковой фазе. По этой причине фронт волны является одной из волновых поверхностей.
Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне, распространяющейся вдоль оси ОХ, все величины, характеризующие колебательное движение среды, зависят только от времени t и координаты х рассматриваемой точки М среды. Если нет поглощения волн в среде, то колебания в точке М отличаются от колебаний в начале координат О только тем, что они сдвинуты по времени на ∆t. Уравнение плоской синусоидальной волны, распространяющейся в непоглощающей среде вдоль положительного направления оси ОХ,
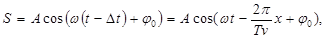 (4.54)
(4.54)
где А=const - амплитуда колебаний, называемая амплитудой волны; ω=2π/T - циклическая (круговая) частота волны; Т - период колебаний, а φ o - начальная фаза колебаний (в момент времени t=0) в точках координатной плоскости x =0. Расстояние
λ= v Т, (4.55)
на которое распространяется синусоидальная волна за время, равное периоду колебаний, называется длиной волны. Длина волны равна расстоянию между двумя ближайшими точками среды, в которых разность фаз колебаний равна 2π.
Наряду с длиной волны используется другая характеристика синусоидальной волны - волновое число:
 (4.56)
(4.56)
Поэтому уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси ОХ, можно также представить в виде
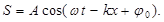 (4.57)
(4.57)
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер. Центр этих сфер называется центром волны. Такого рода волны возбуждаются в однородной изотропной среде уединенным точечным источником. Уравнение расходящейся синусоидальной сферической волны имеет вид
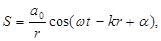 (4.58)
(4.58)
где r – расстояние от центра волны до рассматриваемой точки М среды; А(r)= а o/ r - амплитуда волны; α o - физическая величина, численно равная амплитуде волны на единичном расстоянии от ее центра; α – начальная фаза колебаний в центре волны.
Реальные источники волн всегда имеют конечные размеры. Однако их можно считать точечными, а волны, возбуждаемые ими в однородной изотропной среде, - сферическими, если расстояние r от источника до рассматриваемых точек среды значительно больше размеров источника. Если r очень велико, то любые малые участки волновых поверхностей практически можно считать плоскими.
Скорость v распространения синусоидальной волны называется фазовой скоростью. Она равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы синусоидальной волны. Например, в случае плоской синусоидальной волны из условия ω t+kx + φ o=const следует, что
 (4.59)
(4.59)
 2014-02-02
2014-02-02 2976
2976
