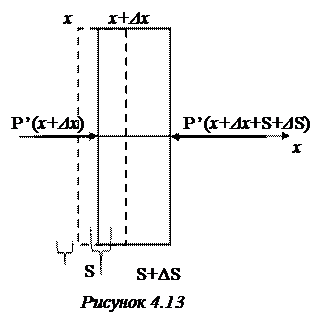2014-02-02
2424
По отношению к деформациям растяжения и сжатия газ является упругой средой, в нем могут распространяться продольные волны. Рассмотрим распространение в газе вдоль оси х плоской продольной волны. Выделим в газе слой толщиной Δх и единичной площади, перпендикулярный оси (рис. 4.13). В данном случае роль нормального напряжения σ, т.е. силы, действующей на единицу площади слоя, играет давление газа Р’, которое может быть представлено как сумма
Р’= Р + ΔР, (4.71)
где Р – среднее давление газа, а ΔР – периодически изменяющееся отклонение от среднего значения. Повторяя рассуждения, которые привели к формуле (4.66) для силы, действующей на слой единичной площади, получим в данном случае
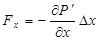. (4.72)
Использование этого выражения во втором законе Ньютона приведет к уравнению
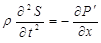, (4.73)
где ρ – плотность газа. При распространении в газе звуковой волны процессы сжатия и расширения происходят настолько быстро, что их можно считать адиабатическими. Для выделенного слоя газа можно записать уравнение Пуассона
.
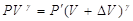Из рисунка 4.13 видим, что объем недеформированного слоя единичной площади V численно равен его толщине Δx, а изменение объема ΔV – величине ΔS. С учетом этого уравнение Пуассона можно представить в виде
.
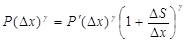После сокращения и перехода к пределу Δх → 0 получаем
.
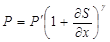Будем рассматривать случай, когда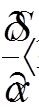 
, что соответствует малости изменения толщины слоя газа по сравнению с самой толщиной. В этом случае
,
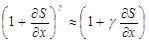а
.
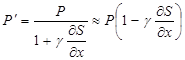Дифференцируем последнее выражение по х и получаем
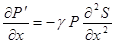. (4.74)
Подстановка выражения (4.74) в выражение (4.73) приводит к уравнению
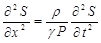. (4.75)
Коэффициент перед второй производной величины S по времени можно преобразовать с помощью уравнения Менделеева-Клапейрона
,
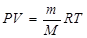где m – масса газа, М – его молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура. Отсюда следует:
.
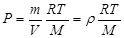Подстановка этого выражения в формулу (4.75) приводит волновое уравнение для газов к его окончательной форме
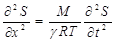. (4.76)
Сравнение формулы (4.76) с формулой (4.60) позволяет получить формулу для скорости распространения звука в газе
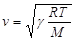. (4.77)
Вычисление по этой формуле скорости звука в воздухе при нормальных условиях дает значение 340 м/c.
