2014-02-02
248
Метод динамического программирования.
Рассмотрим систему
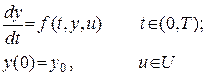(4.1)
и функционал
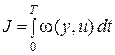(4.2)
который требуется минимизировать. Правый конец фазовых координат является свободным.
Наряду с этой вариационной задачей рассмотрим вспомогательную, когда процесс рассматривается в интервале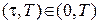 
и минимизируется функционал
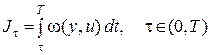. (4.3)
Пусть сначала найден минимум J (4.2) и соответствующее ему оптимальное управление (рис. 1а):
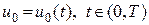(4.4)
а потом – минимум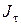 
(4.3) и оптимальное управление (рис. 1б):
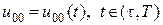. (4.5)
В последнем случае предполагается, что в момент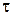 
процесс начинается с состояния 
, достигнутого к моменту времени 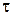при оптимизации процесса в интервале 
.
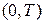Вообще говоря, управления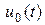 
и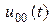 
отличаются интервалом и значениями. Принцип оптимальности утверждает, что оптимальные управления 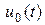и 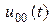в общей части интервала 
совпадают, не зависимо от предыстории процесса и вполне определяются состоянием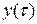 
в момент 
.
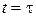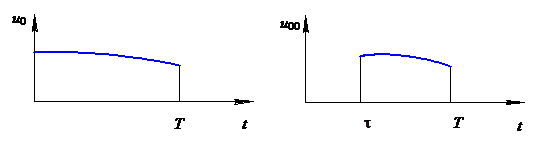
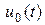В случае со свободным правым концом принцип оптимальности доказывается. В самом деле, допустим, что на участке управления и 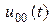не совпадают и
 |
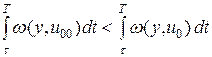. (4.6)
Рис. 1 а Рис.1 б
Тогда для первой задачи введем управление
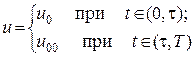(4.7)
и вычислим функционал
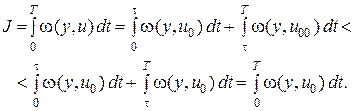
При управлении u (4.7) функционал(4.2) принимает меньшее значение, чем при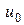 
(4.4). Но управление 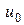является оптимальным. Поэтому допущение (4.6) неверно.
A предположение
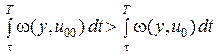
противоречит тому, что 
- управление, минимизирующее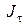 
(4.3).
Таким образом, остается, что
,
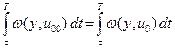и если оптимальное управление единственное, то
.
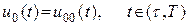Кратко принцип оптимальности можно сформулировать так: последний участок оптимальной траектории является оптимальным независимо от предыстории процесса.
