Для виробництва двох виробів А і В підприємство використовує три типи технологічного обладнання. Кожний з виробів повинен пройти обробку на даному типі обладнання. Час обробки кожного з виробів, витрати, пов’язані з виробництвом одного виробу, наведено у таблиці. Обладнання 1-го та 3-го типів підприємство може використовувати не менше 48 і 6 годин відповідно, а обладнання 2-го типу не більше 50 годин.
| Тип обладнання | Витрати часу на обробку одного виробу, год. | |
| А | В | |
| Витрати на виробництво одного виробу, тис. грн.. |
Визначити обсяг виробництва продукції за умови найменшої середньої собівартості одного виробу.
4. Графічне розв’язання задачі дробово-лінійного програмування.
У загальному випадку цільова функція задачі дробово-лінійного програмування має вигляд
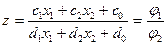 (13)
(13)
З огляду на те, що 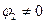 , тобто
, тобто 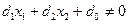 , можна записати
, можна записати
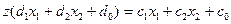 (14)
(14)
З рівняння (13) виразимо змінну х2 через х1
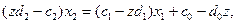 (15)
(15)
або
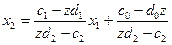 (16)
(16)
Останнє рівняння можна розглядати як рівняння прямої 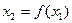 з кутовим коефіцієнтом
з кутовим коефіцієнтом  . З виду k можна зробити висновок, що при зміні значення цільвої функції z, змінюється k- кут нахилу лінії рівня. На відміну від задачі ЛП, щоб досягти оптимального значення z, лінію рівня потрібно повертати, а не переміщувати паралельно самій собі. Залишилося з’ясувати два питання:
. З виду k можна зробити висновок, що при зміні значення цільвої функції z, змінюється k- кут нахилу лінії рівня. На відміну від задачі ЛП, щоб досягти оптимального значення z, лінію рівня потрібно повертати, а не переміщувати паралельно самій собі. Залишилося з’ясувати два питання:
· як повертати: за годинковою стрілкою або проти годинкової стрілки;
· навколо якої точки здійснювати поворот.
Звернемо увагу на те, що
 . (17)
. (17)
Кутовий коефіцієнт є функцією z. Щоб визначити, як повертати лінію рівня для досягнення zmax або zmin, необхідно дослідити функцію k(z) на монотонність.
Обчислемо похідну
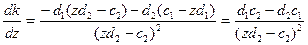 (18)
(18)
· якщо 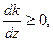 то k зростає при збільшенні z;
то k зростає при збільшенні z;
· якщо 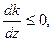 то k спадає при збільшенні z..
то k спадає при збільшенні z..
Таким чином, якщо
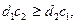 (19)
(19)
то 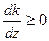 й при збільшенні z лінія рівня повертається проти годинникової стрілки.
й при збільшенні z лінія рівня повертається проти годинникової стрілки.
Якщо
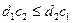 (20)
(20)
то 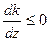 й збільшенні z лінія рівня повертається за годинниковою стрілкою.
й збільшенні z лінія рівня повертається за годинниковою стрілкою.
З рівняння (15) випливає, що при 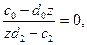 тобто при
тобто при 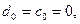 лінія рівня проходить через початок координат і, отже, поворот здійснюється навколо початку координат.
лінія рівня проходить через початок координат і, отже, поворот здійснюється навколо початку координат.
Якщо, 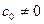 й/або
й/або 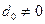 , то рівняння (15) визначає пучок прямих, які проходять через деяку точку
, то рівняння (15) визначає пучок прямих, які проходять через деяку точку 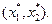 Рівняння пучка прямих, які проходять через задану точку
Рівняння пучка прямих, які проходять через задану точку 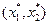 з урахуванням (15), запишеться у вигляді:
з урахуванням (15), запишеться у вигляді:
 (21)
(21)
Так як з (15) маємо
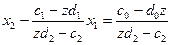 (22)
(22)
То підставивши (21) в (20), одержимо
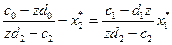 (23)
(23)
звідки
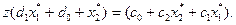 (24)
(24)
Останнє рівняння повинне виконуватися для всіх значень z. Це можливо, тільки якщо
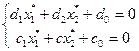 (25)
(25)
Таким чином, у випадку якщо 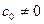 й/або
й/або 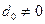 , поворот лінії рівня здійснюється навколо точки з координатами
, поворот лінії рівня здійснюється навколо точки з координатами 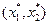 , які є розв’язком системи (25).
, які є розв’язком системи (25).
Установивши напрям повороту, знаходимо вершину або вершини багатокутника розв’язків, у яких функція приймає екстремальне значення, або встановлюємол необмеженість значення цільової функції задачі.
Питання для самоконтролю.
· Сформулюйте задачу дробово-лінійного програмування.
· Дайте економічну інтерпретацію задачі дробово-лінійного програмування.
· Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування.
· У чому принципова відмінність геометричної інтерпретації задачі дробово-лінійного програмування?
· Навколо якої точки здійснюється поворот лінії рівня?
· Сформулюйте алгоритм розв’язання задачі дробово-лінійного програмування графічним методом.
Тема 6. Нелінійні оптимізаційні моделі економічних систем
Лекція 8
Тема лекції: Задачі нелінійного програмування
Мета: ознайомити студентів з методами розв’язання задач нелінійного програмування.
План лекції
1. Постановка задачі пошуку екстремуму функції.
2. Властивості випуклих множин та випуклих функцій.
3. Необхідні та достатні умови безумовного екстремуму функції.
4. Умовний екстремум при обмеженнях типу рівність.
Література:
1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
1. Постановка задачі пошуку екстремуму функції.
Знайти такий вектор 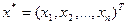 , що належить області допустимих рішень
, що належить області допустимих рішень 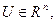 цільова функція від якого
цільова функція від якого
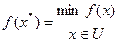
Зауваження:
1. Пошук максимуму функції зводиться до задачі визначення мінімуму функції шляхом заміни знака перед функцією на протилежний: 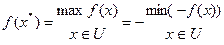
2. Задача пошуку максимуму та мінімуму цільової функції зветься задачею пошуку екстремуму: 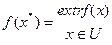
3. Якщо безліч допустимих рішень U задається обмеженнями, що накладаються на вектор х, то вирішується завдання пошуку умовного екстремуму. Якщо, обмеження на вектор х відсутні, то вирішується завдання пошуку безумовного екстремуму.
4. Рішенням задачі пошуку екстремуму є пара  яка включає точку х* та значення цільової функції f в цій точці.
яка включає точку х* та значення цільової функції f в цій точці.
Нагадаємо, що точка 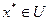 зветься точкою глобального мінімуму (або просто мінімуму), якщо на множені U функція досягає свого мінімального значення, тобто
зветься точкою глобального мінімуму (або просто мінімуму), якщо на множені U функція досягає свого мінімального значення, тобто 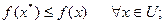
точка 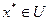 зветься точкою локального мінімуму функції f на множені U, якщо
зветься точкою локального мінімуму функції f на множені U, якщо 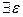 >0, що
>0, що 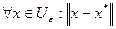 <
<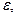 то
то 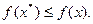
Тут 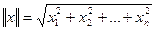 - евклідова норма вектора х.
- евклідова норма вектора х.
Загальна задача нелінійного програмування полягає у знаходженні максимального(мінімального) значення функції
Z=f(x1, x2,….. xn) →max/ min (1)
за умов
gi(x1, x2,….. xn) { ≤=≥}bi, i=1,2…..m (2)
де всі функції (або їх частина) нелінійні.
Функція f з (1) – цільова функція, а умови gi з (2) - умовами обмеження.
Сукупність змінних, що задовольняють обмеженням (2) задачі називається допустимим розв’язком або планом. Кожному допустимому розв ’ язкувідповідає певне значення цільової функції.
Допустимий розв ’ язок (план), при якому цільова функція набуває найбільшого (найменшого) значення називається оптимальним планом. Найбільше (найменше) значення функції в допустимій області розв’язків називається глобальним максимумом (мінімумом).
Означення 1. Поверхнею рівня функції f(х) називається множина точок, в яких функція приймає постійне значення, тобто f(х)=const. Якщо n=2, то поверхня рівня зображується лінією рівня на площині R2.
Приклад 1. Побудувати лінію рівня функцій:
a) 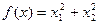
b) 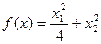
c) 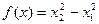 .
.
Означення 2. Градієнтом 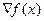 безперервно диференційованої в точці х функції f(х) зветься вектор - стовпець, елементами якого є часткові похідні першого порядку, обчислені в точці х:
безперервно диференційованої в точці х функції f(х) зветься вектор - стовпець, елементами якого є часткові похідні першого порядку, обчислені в точці х:
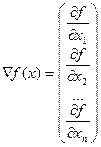
Градієнт функції направлений по нормалі до поверхні рівня, тобто перпендикулярний до дотичної площини, проведеної в точці х, у бік найбільшого зростання функції в даній точці.
Означення 3. Матрицею Гессе Н (х) двічі неперервно диференційованою в точці х зветься матриця часткових похідних другого порядку, обчислених в точці:
Н= 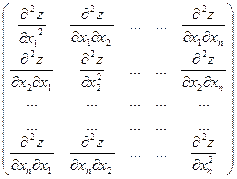 =
=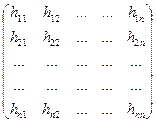
Зауваження:
1. Матриця Гессе є симетричною матрицею розміром nxn.
2. Разом з градієнтом можна визначити вектор антіградіента, рівний за модулем вектору градієнта, але протилежного за напрямком. Він вказує у бік найбільшого спуску функції в даній точці.
3. За допомогою градієнта та матриці Гессе, використовуючи розкладання в ряд Тейлора, приріст функції f(x) може бути записано у формі:
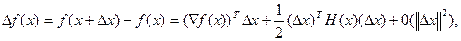 (2)
(2)
де  - сума всіх членів розкладання в ряд Тейлора, які мають порядок вище другого,
- сума всіх членів розкладання в ряд Тейлора, які мають порядок вище другого, 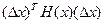 - квадратична форма.
- квадратична форма.
 2014-02-02
2014-02-02 870
870








