Задания к практическим занятиям
Критерии качества разбиения выборки на классы
Классификация многомерных наблюдений методом k - средних
Иерархический метод классификации
Меры сходства групп объектов (классов)
Другой важной величиной в кластерном анализе является расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов. Пусть 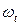 — t -я группа (класс, кластер) объектов,
— t -я группа (класс, кластер) объектов, 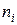 — число объектов, образующих группу
— число объектов, образующих группу 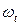 , вектор
, вектор 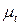 — среднее арифметическое объектов, входящих в группу
— среднее арифметическое объектов, входящих в группу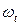 (другими словами
(другими словами 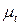 — “центр тяжести” t -й группы), a
— “центр тяжести” t -й группы), a 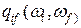 — расстояние между группами
— расстояние между группами 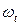 и
и 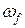 .
.
Наиболее распространенными методами определения расстояния между кластерами 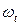 и
и 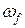 являются: метод “ближайшего соседа” (1), метод “дальнего соседа” (2), метод оценки расстояния между центрами тяжести (3). Графическое представление оценки расстояния различными методами приведено на рис. 7.5.
являются: метод “ближайшего соседа” (1), метод “дальнего соседа” (2), метод оценки расстояния между центрами тяжести (3). Графическое представление оценки расстояния различными методами приведено на рис. 7.5.
|
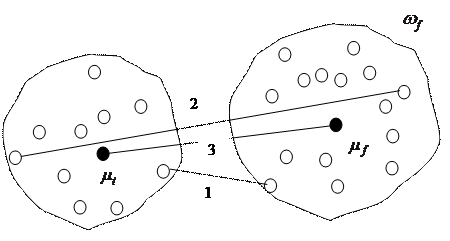
Рис. 7.5. Расстояния между классами (1 - метод “ближайшего соседа”, 2 - метод “дальнего соседа” 3 - метод оценки расстояния между центрами тяжести)
Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров:
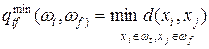 (7.14)
(7.14)
Расстояние дальнего соседа — расстояние между самыми дальними объектами кластеров:
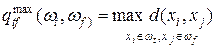 (7.15)
(7.15)
Расстояние центров тяжести равно расстоянию между центральными точками кластеров:
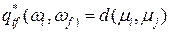 (7.16)
(7.16)
Обобщенное (по Колмогорову) расстояние между классами, или обобщенное k - расстояние, вычисляется по формуле
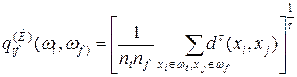 (7.17)
(7.17)
Выбор той или иной меры расстояния между кластерами влияет, главным образом, на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.
Среди всех методов классификации самым распространенными являются иерархические агломеративные методы. Основная идея этих методов состоит в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Иерархическая процедура состоит в пошаговом объединении наиболее близких классов. Близость классов оценивается по матрице расстояний или матрице сходства. На первом шаге матрица сходства имеет размерность 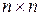 . На следующем шаге при объединении двух классов матрица сходства пересчитывается. Размерность матрицы сокращается на единицу и становится
. На следующем шаге при объединении двух классов матрица сходства пересчитывается. Размерность матрицы сокращается на единицу и становится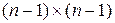 ). Процесс завершается за
). Процесс завершается за 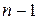 шагов, когда все объекты будут объединены в один класс. Заметим, что при расчете матрицы сходства на очередном шаге необходимо пересчитать только один столбец и строку матрицы. Расстояние между классами может быть рассчитано различными способами (см. предыдущий параграф).
шагов, когда все объекты будут объединены в один класс. Заметим, что при расчете матрицы сходства на очередном шаге необходимо пересчитать только один столбец и строку матрицы. Расстояние между классами может быть рассчитано различными способами (см. предыдущий параграф).
Процесс объединения объектов можно изобразить в виде графа-дерева (дендрограммы). На дендрограмме указываются номера объединяемых объектов и расстояния, при которых произошли объединения. При выделении классов руководствуются скачками метрики сходства на дендрограмме.
Рассмотрим пример решения задачи классификации с помощью иерархического агломеративного алгоритма. Расчеты были выполнены на основании данных таблицы (рис. 7.6). Диаграмма рассеивания признаков 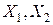 представлена на рис. 7.7. На диаграмме визуально выделяются три класса. Убедимся, на примере, как объединит объекты в классы, рассматриваемый алгоритм.
представлена на рис. 7.7. На диаграмме визуально выделяются три класса. Убедимся, на примере, как объединит объекты в классы, рассматриваемый алгоритм.
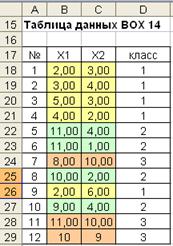
Рис. 7.6. Таблица данных
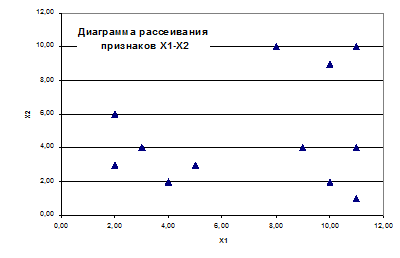
Рис. 7.7. Диаграмма рассеивания признаков 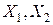
На первом шаге рассчитывается матрица расстояний между объектами (евклидовы расстояния рис. 7.8). Матрицу расстояний рассчитываем с помощью макроса “Расстояния”. В матрице расстояний мы заменили диагональные элементы (нулевые значения) на значение заведомо большее, чем все остальные элементы матрицы (в нашем случае 100). Такая замена удобна для расчета минимального значения матрицы с помощью функции МИН.
Находим минимальное значение матрицы расстояний (1,414). Объединим объекты 1-2 в один класс. В новой матрице необходимо рассчитать расстояния от класса (1-2) до всех остальных объектов. Расстояние будем рассчитывать по методу ближайшего соседа. Для этого из двух расстояний рис. 7.9 необходимо выбрать минимальные значения. В результате будет получена новая таблица – рис. 7.10.
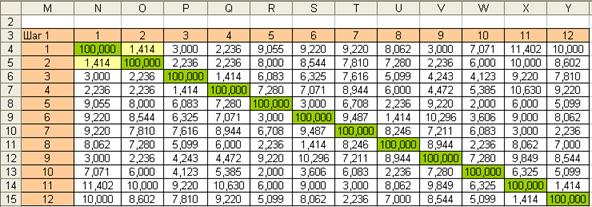
Рис. 7.8. Матрица расстояний (Шаг 1)
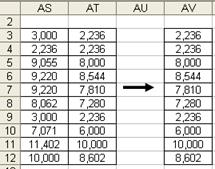
Рис. 7.9. Расчет расстояний от класса (1-2) до всех остальных объектов
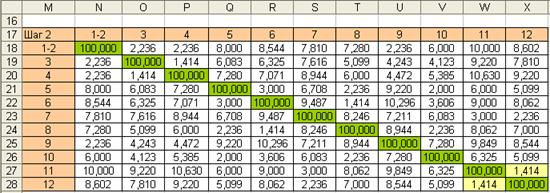
Рис. 7.10. Матрица расстояний (Шаг 2)
Далее процесс объединения классов продолжается. На рис. 7.11 приведены расчеты при выполнения алгоритма на шагах 3-11. Процесс объединения объектов представлен на дендрограмме рис. 7.12. По дендрограмме можно обнаружить, что на определенном этапе происходит скачек расстояния, объединяемых классов. Этот скачек согласуется с классификацией объектом при визуальном анализе диаграммы рассеивания объектов. Студентам предлагается повторить расчеты, используя при расчете расстояний между классами объектов ”метод дальнего соседа”.
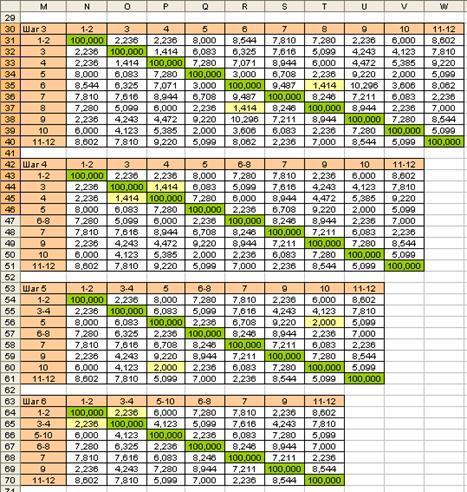
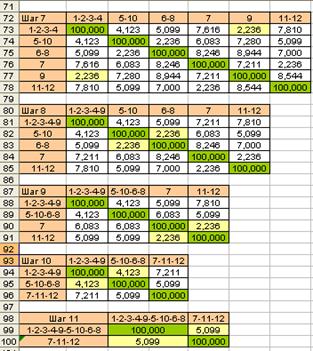
Рис. 7.11. Расчет матриц расстояний на шагах 7-11

Рис. 7.12. Дендрограмма объединения объектов
Методом k - средних был предложен Мак-Куином. Этот метод классификации относится к группе итеративных методов классификации. Этот метод является одним из самых простых. Существует множество модификаций этого метода. Рассмотрим алгоритм классификации в его первоначальном виде.
Пусть имеется n объектов (наблюдений), каждый из которых характеризуется m признаками 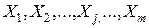 . Необходимо разбить наблюдения на заданное число классов - k.
. Необходимо разбить наблюдения на заданное число классов - k.
Шаг ноль. Из n точек исследуемой совокупности случайным образом отбирается k точек. Эти точки принимаются как центры классов.
Итерация. Множество точек разбивается на k классов по минимуму расстояния до центров классов. Для расчета расстояния можно использовать любую метрику. Чаще всего используется евклидово расстояние. Производится пересчет центров классов, как центров тяжести точек, присоединенных к классам.
Проверка. Если центры классов при выполнении очередной итерации не изменились, то процесс классификации завершается, иначе переходим к пункту ”Итерация”.
Рассмотрим работу алгоритма на примере. Таблица данных представлена на рис. 7.13. Для формирования таблицы мы смоделировали выборку из трех классов. Объемы выборок по классам равны соответственно 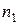 =10,
=10, 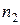 =15,
=15,  =20. Всего объектов в выборке
=20. Всего объектов в выборке 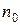 =45.
=45.

Рис. 7.13. Таблица данных
Классы в таблице располагаются один под другим. Исходная выборка представлена на диаграмме рассеивания рис. 7.14. Теперь забудем о том, что наша выборка разделена на классы и попытаемся выполнить классификацию объектов с помощью алгоритма.
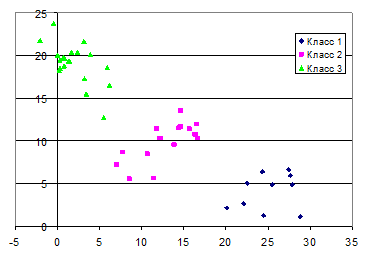
Рис. 7.14 Диаграмма рассеивания исходной выборки
Первоначальный выбор центров классов производим с помощью случайных чисел. Координаты центров классов по итерациям заносим в таблицу (рис. 7.15).
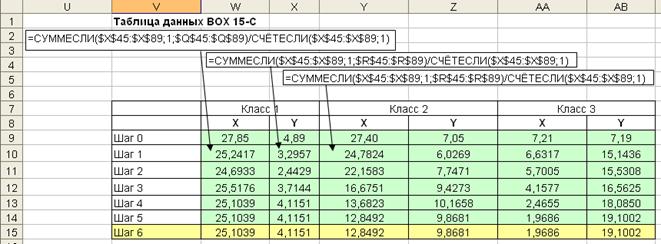
Рис. 7.15. Таблица центров классов по шагам
На каждом шаге рассчитывается пять столбцов таблицы. Первые три – это расстояния до центров классов (“Расстояние 1”, “Расстояние 2”, “Расстояние 3”). Четвертый столбец содержит минимум из трех расстояний. На основании информации четырех столбцов определяется номер класса объекта (столбец ”Класс”) по расстоянию до ближайшего центра (рис. 7.16). Итерация завершается пересчетом центров классов. Расчет новых центров классов производится с применением функций СУММЕСЛИ и СЧЕТЕСЛИ (рис. 7.15). Расчет повторяется до тех пор, пока центры классов перестают изменяться. В нашем случае результат получен за шесть шагов.
Результаты классификации на первом и третьем шаге прдставлены на диаграммах рассеивания рис. 7.-17-7.18.
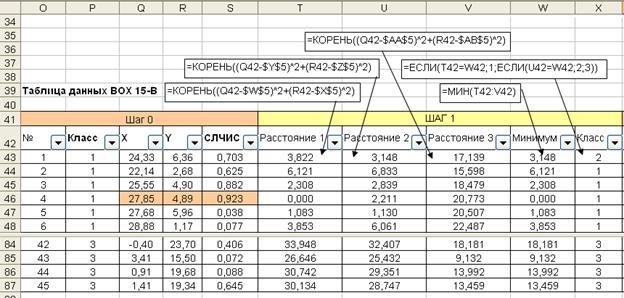
Рис.7.16. Расчет номеров класса на одном шаге итерационного процесса
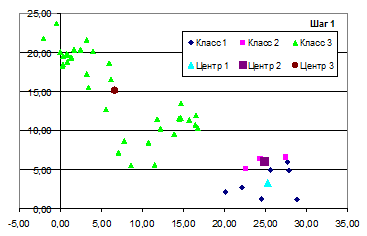
Рис. 7.17. Классификация объектов на шаге 1
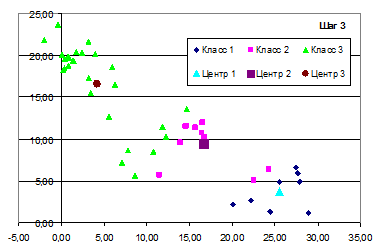
Рис. 7.18. Классификация объектов на шаге 3
Смещение центров классов по итерациям представлено на рис. 7.19. Применение алгоритма к данным примера дало безошибочный результат. На практике алгоритм далеко не всегда дает такой хороший результат. В нашем примере, сформированные классы, очень хорошо различимы.
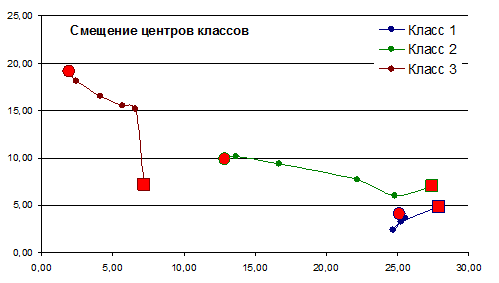
 Рис. 7.19. Смещение центров классов по итерациям (- начальное расположения центра класса
Рис. 7.19. Смещение центров классов по итерациям (- начальное расположения центра класса
 – конечное расположение центра класса)
– конечное расположение центра класса)
7.6. Классификация многомерных наблюдений методм – KRAB
 2014-02-03
2014-02-03 3120
3120








