Изменение геометрических характеристик при параллельном переносе координатных осей

Пусть известны геометрические характеристики сечения относительно осей ХY. Требуется определить геометрические характеристики сечения относительно осей Х₁Y₁. Известно, что оси этих двух систем координат параллельны (рис.10). Координаты любой точки в новой системе координат можно выразить через координаты в прежней системе координат следующим образом:

х₁ =х-а, (9)

у₁=у-b.

Рис. 10

Запишем геометрические характеристики в новой системе координат по определению и сделаем замену «новых» координат на предыдущие:

S_х1=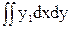==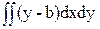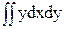-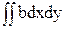= S_х – bF;

S_у1=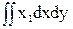==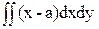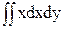-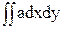= S_y – aF;

I_х1====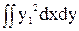

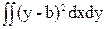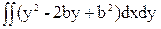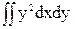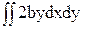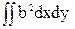=-+= I_х-2bS_х + b²F; (10)

I_у1====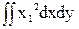

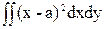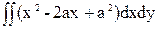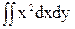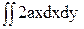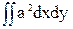=-+= I_y-2aS_y + a²F;

I_х1у1====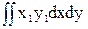

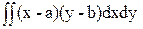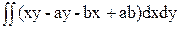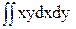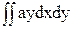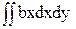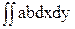=--+= I_ху - aS_y – bS_x + abF.

Необходимо помнить, что координаты а и b, входящие в формулы, необходимо подставлять с учетом их знака.

Рассмотрим частный случай. Пусть оси Х₁Y₁ – центральные, тогда

S_х1= S_х - bF=0,

S_у1= S_у - аF=0.

Следовательно

b=S_х/F=у_с, (11)

a=S_y/F=х_с,

где х_с, у_с - координаты центра тяжести сечения в произвольной системе координат ХY.